GuruGuia

Questão 33390

IME

[IME - 2014/2015 - 1a fase]

A figura acima apresenta um circuito elétrico e um sistema de balança. O circuito é composto por uma Fonte em U cinco resistores, um capacitor, um quadrado formado por um fio homogêneo, duas chaves e um eletroímã interligados por fios de resistência desprezível. O sistema de balança é composto por um bloco e um balde de massa desprezível que está sendo preenchido por água através de um dispositivo. Sabe-se que, imediatamente após o carregamento do capacitor, a chave Ch_a se abrirá e a chave Ch_b se fechará, fazendo com que o capacitor alimente o eletroímã, de modo que este acione um dispositivo que interromperá o fluxo de água para o balde. O valor do capacitor para que o sistema balde e bloco fique em equilíbrio e a energia dissipada no fio a partir do momento em que o capacitor esteja completamente carregado até o vigésimo segundo são, respectivamente

Dados:

- U = 100V

- resistência total do fio: 32 K $Omega$

- fluxo de água: 200 ml/s

- massa específica da água = 1g/cm³

- massa do bloco: 0,8 Kg

Observações:

- despreze a massa do balde;

- considere o capacitor carregado em um tempo correspondente a cinco vezes a constante de tempo.

$6mu F$ e 10J

$8mu F$ e 10 J

$8mu F$ e 20 J

$10mu F$ e 10 J

$10mu F$ e 20 J

Gabarito:

$8mu F$ e 20 J

Resolução:

Primeiramente, vamos determinar a o tempo necessário para que a água do balde equilibre o bloco:

$0,2_{ kg/s} cdot t = 0,8kg ightarrow t = 4s$

Sendo a constante de tempo do circuito dada por RC, então:

$4 = 5 RC$

$RC = frac 45 s= 0,8s$

$R_{ab} = R_h = [(12 / / 4)+97]k Omega$

$R_{ab} =100k Omega$

$0,8 = 100 cdot 10^3 cdot C$

$C = 8 cdot 10^{-6}F$

Na situação em que o capacitor está totalmente carregado, teremos um tempo decorrido igual a:

$5 cdot 100 cdot 10^3 cdot 8 cdot 10^{-6 } = 4s$

Assim, deve ser calculada a energia dissipada no fio em 16s, tal que:

$varepsilon = P cdot Delta t$

$varepsilon = frac {U^2}{R} cdot Delta t$

$varepsilon = frac {100^2}{8 cdot 10^3} cdot 16$

$varepsilon = 20J$

RESOLUÇÃO DOS OFICIAIS DA RESOLUÇÃO

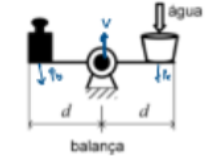
Para aestar em equilíbrio:

F_R = 0

Logo

$F_{B} imes d+F_{c} imes d = 0$

Adotando a rotação antihorária como sentido positivo

$P_{B} imes d-P_{C} imes d = 0$

$P_{B} imes d = P_{C} imes d$

Como g e d são iguais para ambos

$m_{B} = m_{C}$

Sendo

$m_{C} = 200mL ightarrow 200g$

$0,8;kg = 0,2;kg imes Delta t$

$Delta t = 4s$

O capacitor carrega em 4s. Pela teoria dos circuitos

$T_{carga} = 5RC$

$4 = 5RC$

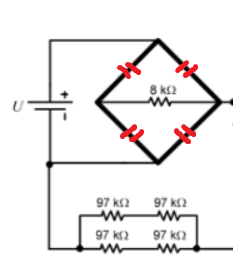
Ponte de Wheatstone

5 resistores de 8 K (vale destacar que a ponte estará em equilíbrio) curto-circuitando a fonte

Resistores associados em série → 97 K + 97 K = 194 K

Resistores associados em paralelo → 194 K / 2 = 97 K

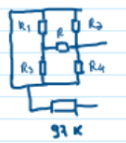
Sendo assim

$R_{eq} = frac{8 K}{2}$

$R_{eq} = 4 K$

R₁ está em paralelo com R₃, assim como R₂ e R₄:

$R_{eq} = frac{1}{frac{1}{12}+frac{12}{4}} = frac{1}{frac{1+3}{12}}$

$R_{eq} = = frac{1}{1}cdot frac{12}{4}$

$R_{eq} = 3KOmega$

$R_{eq} = 3K+ 97K = 100KOmega$

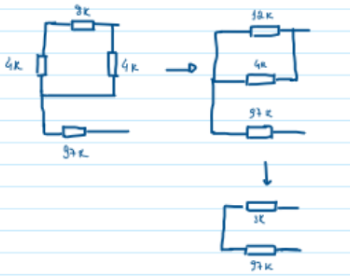
Substituindo na fórmula de tempo de carga:

$4cdot 5 RC$

$4cdot 5 cdot 100cdot 10^{3}C$

$C = frac{4}{500cdot 10^{3}}$

$C = 8cdot 10^{6};C$

$C = 8cdot 10^{6}; mu C$

Potência dissipada:

$P=frac{U^{2}}{R}$

$P=frac{100^{2}}{8cdot 10^{-3}}$

$P=frac{10}{8}$

o tempo de dissipação será

$20-4 = 16$

Logo:

$E = frac{10}{8} cdot 16 = frac{160}{8} = 20 J$

Questão 992

IME

(IME 2007)

O gráfico acima apresenta a velocidade de um objeto em função do tempo. A aceleração média do objeto no intervalo de tempo de 0 a 4t é:

Ver questão

Questão 993

IME

(IME 2007) Um cubo de material homogêneo, de lado L = 0,4 m e massa M = 40 kg, está preso à extremidade superior de uma mola, cuja outra extremidade está fixada no fundo de um recipiente vazio. O peso do cubo provoca na mola uma deformação de 20 cm. Coloca-se água no recipiente até que o cubo fique com a metade de seu volume submerso. Se a massa específica da água é , a deformação da mola passa a ser:

Ver questão

Questão 994

IME

(IME 2007) Uma nave em órbita circular em torno da Terra usa seus motores para assumir uma nova órbita circular a uma distância menor da superfície do planeta. Considerando desprezível a variação da massa do foguete, na nova órbita:

Ver questão

Questão 995

IME

(IME 2007) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderá ser nula se, dentre as opções abaixo, a transformação seguinte for uma:

Ver questão