GuruGuia

Questão 43559

IME

[IME- 2014/2015 - 2ª fase]

Num triângulo ABC isósceles, com ângulos iguais em B e C, o seu incentro I se encontra no ponto médio do segmento de reta que une o seu ortocentro H a seu baricentro G. O segmento de reta AG é menor que o segmento de reta AH. Os comprimentos dos segmentos de reta HI e IG são iguais a d. Determine o perímetro e a área desse triângulo em função de d.

Gabarito:

Resolução:

$[ABC]=3.[AGC]Rightarrow frac{b.BK}{2}=3.frac{b.GL}{2}Rightarrow BK=3GL$

$HM=x, AG=2GM Rightarrow AG=4d+2x$

$frac{HK}{6d+2x}=frac{d+x}{5d+2x}$ $Rightarrow HK = frac{(d+x)(6d+2x0)}{5d+2x}$

$frac{BH}{x}=frac{5d+2x}{d+x}=frac{x(5d+2x)}{d+x}$

$frac{GL}{4d+2x}=frac{d+x}{5d+2x} Rightarrow GL=frac{(4d+2x)(d+x)}{5d+2x}$

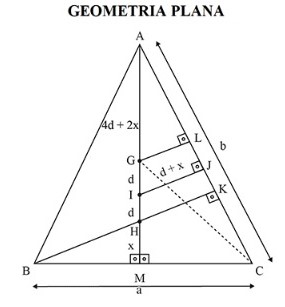
Substituindo BK = 3 GL, temos:

$6d^{3}+39d^{2}x+30dx^{2}+6x^{3}=12d^{3}+30d^{2}x+24dx^{2}+6x^{3}$

$6d^{3}-9d{2}x-6dx^{2}=0 Rightarrow 2d^{2}-3dc-2x^{2}=0$

$Delta =9x^{2}+4.2.2x^{2}=25x^{2}$

$d=frac{3x+5x}{4}2x$

A figura se torna:

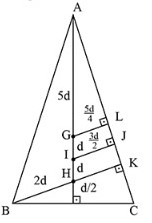
Assim,

$BH=2d Rightarrow a=dsqrt{15}; AM=frac{15d}{2} Rightarrow b=frac{4sqrt{15}d}{2}$

Portanto, o perímetro é:

$a+2b=5dsqrt{15}$

e a área é:

$frac{a.frac{15d}{2}}{2}=frac{15sqrt{15}d^{2}}{4}$

Questão 992

IME

(IME 2007)

O gráfico acima apresenta a velocidade de um objeto em função do tempo. A aceleração média do objeto no intervalo de tempo de 0 a 4t é:

Ver questão

Questão 993

IME

(IME 2007) Um cubo de material homogêneo, de lado L = 0,4 m e massa M = 40 kg, está preso à extremidade superior de uma mola, cuja outra extremidade está fixada no fundo de um recipiente vazio. O peso do cubo provoca na mola uma deformação de 20 cm. Coloca-se água no recipiente até que o cubo fique com a metade de seu volume submerso. Se a massa específica da água é , a deformação da mola passa a ser:

Ver questão

Questão 994

IME

(IME 2007) Uma nave em órbita circular em torno da Terra usa seus motores para assumir uma nova órbita circular a uma distância menor da superfície do planeta. Considerando desprezível a variação da massa do foguete, na nova órbita:

Ver questão

Questão 995

IME

(IME 2007) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderá ser nula se, dentre as opções abaixo, a transformação seguinte for uma:

Ver questão