GuruGuia

Questão 49042

IME

[IME- 2014/2015 - 2ª fase]

Um tetraedro regular, com arestas de comprimento igual a d, é cortado por 2 planos paralelos entre si e a uma das bases, dividindo-o em 3 sólidos de volumes iguais. Determine a altura de cada um destes 3 sólidos em função de d.

Gabarito:

Resolução:

A altura do tetraedro intercepta a base do triangulo no baricentro, que chamaremos de G. O segmento BG mede 2/3 da altura do triângulo BCD.

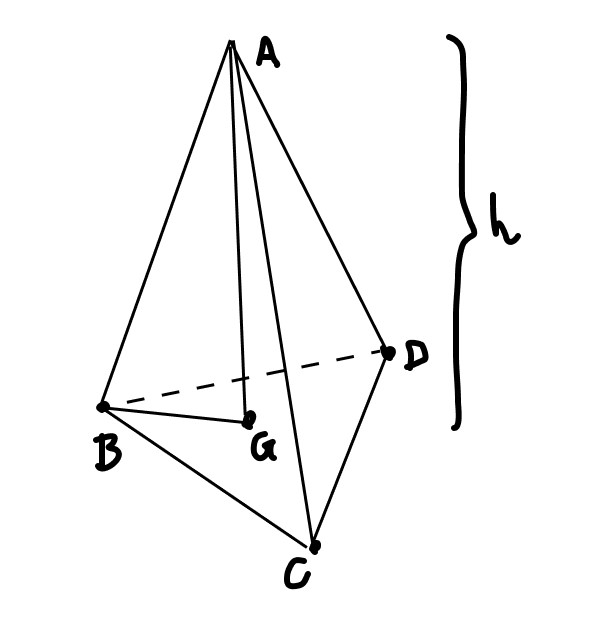Temos que:

$(AB)^{2} - (BG)^{2} = (AG)^{2}$

$(AG)^{2}= d^{2} - (frac{2}{3} cdot frac{dsqrt{3}}{2} )^{2}$

$(AG)^{2} = d^{2} cdot frac{2}{3}$

$AG = frac{dsqrt{6}}{3} = h$

Cortando o tetraedro em três sólidos de igual volume e três alturas diferentes, podemos relacionar proporcionalmente suas alturas e volumes, tal que:

$(frac{h_{1}}{h})^{3} = frac{v_{1}}{V}$

$(frac{h_{1}}{h}) ^{3}= frac{1}{3}$

$h_{1} = frac{1}{sqrt[3]{3}} h$

$h_{1} = frac{1}{sqrt[3]{3}} cdot frac{dsqrt{6}}{3}$

$h_{1} = frac{dsqrt{6} cdot sqrt[3]{9}}{9}$

Da mesma forma, vamos relacionar a soma das alturas h₁e h₂:

$(frac{h_{1} + h_{2}}{h})^{3} = frac{2}{3}$

$h_{1} + h_{2} = frac{sqrt[3]{2}}{sqrt[3]{3}}h$

$h_{1} + h_{2} = frac{sqrt[3]{2}}{sqrt[3]{3}} cdot frac{dsqrt{6}}{3}$

$frac{dsqrt{6} sqrt[3]{9}}{9} + h_{2} = frac{sqrt[3]{2} cdot sqrt[3]{9}cdot dsqrt{6}}{9}$

$h_{2} = (sqrt[3]{2} -1) cdot frac{dsqrt{6} cdot sqrt[3]{9}}{9}$

Calculando a última altura, isto é, a do sólido mais inferior, tal que:

$h_{3} = H - (h_{2} + h_{1})$

$h_{3} = frac{dsqrt{6}}{3} - frac{dsqrt{6} sqrt[3]{9}}{9} (sqrt[3]{2} -1) - frac{dsqrt{6}sqrt[3]{9}}{9}$

$h_{3} = frac{dsqrt{6}}{3} (1 - frac{sqrt[3]{9} (sqrt[3]{2} - 1)}{3} - frac{sqrt[3]{9}}{3})$

$h_{3} = frac{dsqrt{6}}{3} cdot (1-frac{sqrt[3]{18}}{3})$

Questão 992

IME

(IME 2007)

O gráfico acima apresenta a velocidade de um objeto em função do tempo. A aceleração média do objeto no intervalo de tempo de 0 a 4t é:

Ver questão

Questão 993

IME

(IME 2007) Um cubo de material homogêneo, de lado L = 0,4 m e massa M = 40 kg, está preso à extremidade superior de uma mola, cuja outra extremidade está fixada no fundo de um recipiente vazio. O peso do cubo provoca na mola uma deformação de 20 cm. Coloca-se água no recipiente até que o cubo fique com a metade de seu volume submerso. Se a massa específica da água é , a deformação da mola passa a ser:

Ver questão

Questão 994

IME

(IME 2007) Uma nave em órbita circular em torno da Terra usa seus motores para assumir uma nova órbita circular a uma distância menor da superfície do planeta. Considerando desprezível a variação da massa do foguete, na nova órbita:

Ver questão

Questão 995

IME

(IME 2007) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderá ser nula se, dentre as opções abaixo, a transformação seguinte for uma:

Ver questão