GuruGuia

Questão 66980

IME

(IME - 2021/2022)

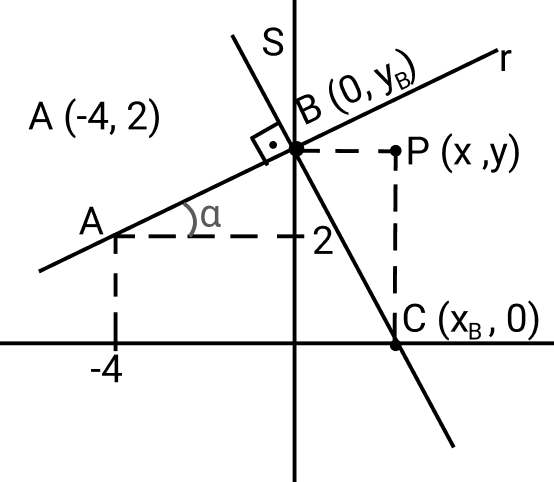
Considere o ponto A(-4,2) e B um ponto variável sobre eixo das ordenadas. Traçam-se as retas AB e por B, a perpendicular a AB que intercepta o eixo das abcissas em C. Seja a equação do lugar geométrico do ponto de interseção da perpendicular ao eixo das abcissas traçada por C com a perpendicular ao eixo das ordenadas traçada por B. A equação desse lugar geométrico é:

$x^2=4y+1$

$y^2=4x$

$y=-x+2$

$x^2+(y-2)^2=4$

$(y-1)^2=4x+1$

Gabarito:

$(y-1)^2=4x+1$

Resolução:

$r : m_{r} = frac{Delta y}{Delta x}=frac{y_{b}-2}{0-(-4)} = frac{y_{b}-2}{4}$

$s: m_{s} = frac{-1}{m_{r}} =frac{4}{2-y_{b}}$

$s:y = m_{s}cdot x+d$

$s cap c : 0 = frac{4}{2-y_{b}}cdot x+y_{b}$

$4x = -y_{b}cdot 2+y_{b}^{2}$

$4x+1=(y_{b}-1)^{2}$

Questão 992

IME

(IME 2007)

O gráfico acima apresenta a velocidade de um objeto em função do tempo. A aceleração média do objeto no intervalo de tempo de 0 a 4t é:

Ver questão

Questão 993

IME

(IME 2007) Um cubo de material homogêneo, de lado L = 0,4 m e massa M = 40 kg, está preso à extremidade superior de uma mola, cuja outra extremidade está fixada no fundo de um recipiente vazio. O peso do cubo provoca na mola uma deformação de 20 cm. Coloca-se água no recipiente até que o cubo fique com a metade de seu volume submerso. Se a massa específica da água é , a deformação da mola passa a ser:

Ver questão

Questão 994

IME

(IME 2007) Uma nave em órbita circular em torno da Terra usa seus motores para assumir uma nova órbita circular a uma distância menor da superfície do planeta. Considerando desprezível a variação da massa do foguete, na nova órbita:

Ver questão

Questão 995

IME

(IME 2007) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderá ser nula se, dentre as opções abaixo, a transformação seguinte for uma:

Ver questão