GuruGuia

Questão 67305

IME

(IME - 2021/2022 - 2ª fase)

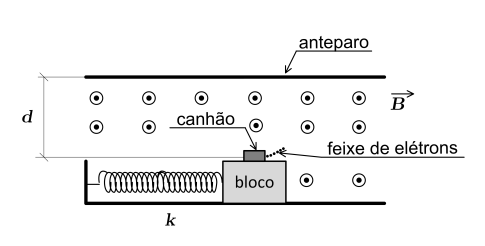
Na figura, encontra-se ilustrado um experimento, em que o canhão preso ao bloco efetua um movimento harmônico simples (MHS) na região sujeita ao campo magnético constante, disparando horizontalmente e continuamente um feixe de elétrons. Nele, observou-se que, nos momentos em que o bloco está com a maior energia cinética, ora os elétrons colidem ortogonalmente contra o anteparo, ora colidem frontalmente contra a traseira do canhão, após tangenciarem o anteparo.

Dados:

velocidade relativa de disparo do feixe de eletrons em relação ao canhão: $v$ ;
constante elástica da mola: $k$ ;
massa do conjunto bloco + canhão: $M$ ;
carga do elétron: $-e$ ;
massa do elétron: $m_e$ ;
distância entre o canhão e o anteparo: $d$ .

Determine:

a) a amplitude de oscilação do bloco para que o experimento seja viável, em função de $v$ , $M$ e $k$ ;

b) o ângulo de impacto entre o anteparo e os elétrons disparados quando o bloco estiver com velocidade nula;

c) a densidade de fluxo magnético do campo $overrightarrow{B}$ , para que o experimento seja viável, em função de $e$ , $m_e$ , $v$ e $d$ ;

d) os possíveis valores de $d$ em relação a $v$ , $M$ e $k$ impostos pelo tempo de viagem dos eletrons até o choque frontal com a traseira do canhão.

Gabarito:

Resolução:

a) Lembrando que, na trajetória circular, a velocidade perpendicular ao campo magnético, o raio é dado por:

$R = frac{mv}{qB}$ , sendo que:

I) Para o raio colidir perpendicularmente:

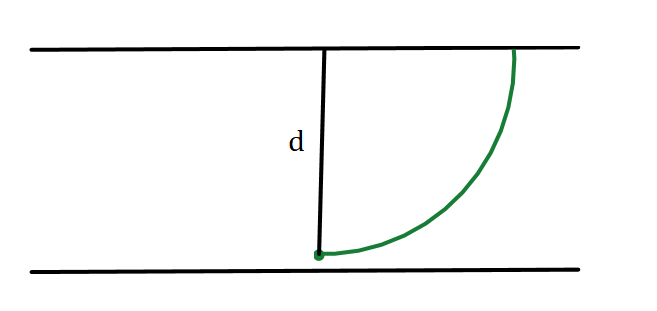
Nesse caso, R = d, então:

$v + wA = frac{eBd}{d}$

II) Para o raio colidir "atrás" (giro 360º):

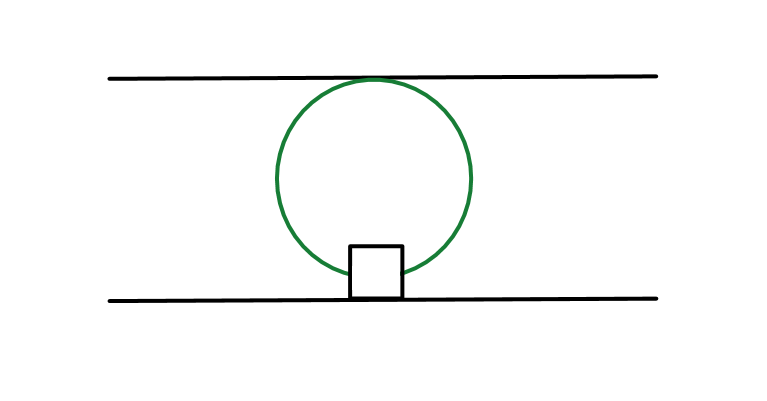
Nesse caso, R = d/2, então:

$v - wA = frac{RB}{m} cdot frac{d}{2}$

Unindo (I) e (II) e resolvendo o sistema:

$v + wA = frac{eBd}{m}$

$v - wA = frac{eB}{m} cdot frac{d}{2}$

Então:

$2v - 2wA = frac{eBd}{m}$

Mas, $w = sqrt{frac{K}{m}}$ , pois T = 2π:

$A = frac{v}{3} cdot sqrt{frac{m}{k}}$

b) Na velocidade nula no MHS, temos:

⇒ os elétrons estão em algum ponto da circunferência entre o 0 e 360º:

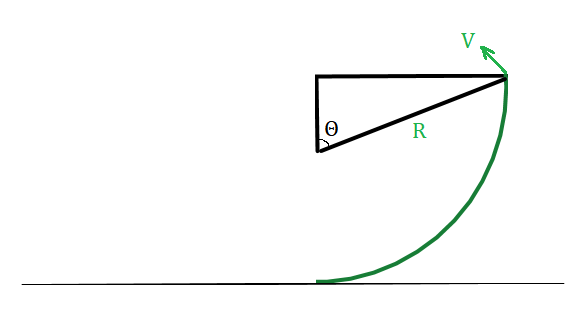
Do triângulo:

$X = R cdot cos heta$

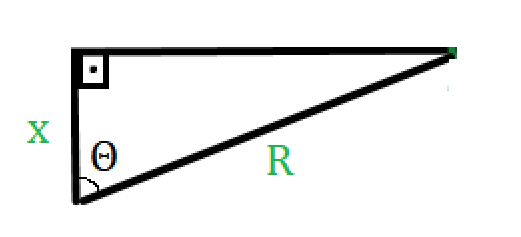
Logo, $d = R + R cdot cos heta$ (Para a posição onde v = 0).

$cos heta = frac{d - R}{R} = frac{d}{R} -1$

Mas:

$frac{d}{R} = frac{4mv}{3eB} cdot frac{1}{R}$

Logo:

$cos heta = frac{1}{3}$

$arccos heta = frac{1}{3}$

c) Basta isolarmos, no item A, o vetor $underset{B}{ ightarrow}$ :

$v + wA = frac{eBd}{m}$

$v - wA = frac{eB}{m} cdot frac{d}{2}$

$2V = frac{3}{2} cdot frac{eBd}{m}$

$underset{B}{ ightarrow} = frac{4mv}{3ed}$

d) Como o nosso perírodo é um multiplo do canhão:

$T = N frac{T_(mhs)}{2}$

$frac{2m}{qB} = N. frac{sqrt M}{sqrt K}$

$frac{3d}{2v} = N. frac{sqrt M}{sqrt K}$

$d = frac{2}{3}.N. frac{sqrt K}{sqrt M}$

Questão 992

IME

(IME 2007)

O gráfico acima apresenta a velocidade de um objeto em função do tempo. A aceleração média do objeto no intervalo de tempo de 0 a 4t é:

Ver questão

Questão 993

IME

(IME 2007) Um cubo de material homogêneo, de lado L = 0,4 m e massa M = 40 kg, está preso à extremidade superior de uma mola, cuja outra extremidade está fixada no fundo de um recipiente vazio. O peso do cubo provoca na mola uma deformação de 20 cm. Coloca-se água no recipiente até que o cubo fique com a metade de seu volume submerso. Se a massa específica da água é , a deformação da mola passa a ser:

Ver questão

Questão 994

IME

(IME 2007) Uma nave em órbita circular em torno da Terra usa seus motores para assumir uma nova órbita circular a uma distância menor da superfície do planeta. Considerando desprezível a variação da massa do foguete, na nova órbita:

Ver questão

Questão 995

IME

(IME 2007) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderá ser nula se, dentre as opções abaixo, a transformação seguinte for uma:

Ver questão