Questão 67308
IME
(IME - 2021/2022 2º Fase)
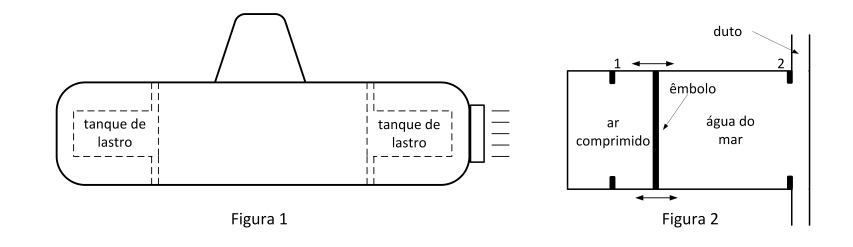
O submarino, mostrado na Figura 1, está com os tanques de lastro vazios de água e, nestas condições, possui massa específica µs = 0,92 g/cm3, quando está sem tripulação e suprimentos. Na Figura 2, ilustra-se um dos dois tanques cilíndricos de lastro idênticos, que podem ser preenchidos com água do mar. Os êmbolos são acionados por motores elétricos, sendo movimentados entre os batentes, de modo a regular o volume de água do mar nesses tanques. Considere que o tanque de lastro esteja sem água com o êmbolo na posição 2 e com 59,5 m3 de água do mar com o êmbolo na posição 1, quando estiver cheio.
Dados:
• massa específica da água do mar: µa = 1,03 g/cm3;
• volume do submarino: Vs = 840 m3; e
• aceleração da gravidade: g = 10 m/s2.
Observação:
• os fluxos de água nos dutos dos tanques de lastro não interferem no movimento do submarino. Admitindo que, em determinada missao, embarcaram tripulantes e suprimentos, perfazendo uma massa de 5880 kg, determine:
a) a porcentagem do volume do submarino que ficará submersa após o embarque, supondo os tanques de lastro com os êmbolos na posição 2;
b) a massa total de água do mar, em kg, que deverá ser introduzida nos tanques de lastro para que ocorra a completa submersão do submarino;
c) os maximos módulos das acelerações verticais, em m/s2 , para emergir e para submergir o submarino, desconsiderando a forc¸a de resistência da água do mar e estando o submarino estabilizado em determinada profundidade.
Gabarito:
Resolução:
Segundo o enunciado, a massa específica do submarino vazio é 0,92 t/m³.
Como o submarino tem um volume de 840 m³, então a massa do submarino é de 772,8 t.
A massa adicionada é de 5,88 t.
Logo, a massa total do submarino inicialmente é M = 778,68 t.
Lembrando da equivalência 1g/cm³ = 1t/m³ e que 1t = 1000kg
a) Supondo o equilíbrio entre a força de empuxo e a força Peso:
Logo,
Dividindo a expressão pelo volume total do submarino:
90% do volume do submarino está submerso
b) Na situação de submersão completa teremos , e supondo que ainda exista o equilíbrio:
Isso implica que há 43,26 t de água em cada um dos tanques.
Portanto, há em cada um dos tanques uma massa d’água de 43260 kg.
A densidade da água do mar é 1,03 t/m³.
Logo, o volume de água em cada um dos tanques é de
c) Para submergir com máxima aceleração, os tanques devem estar completamente cheios de água e para emergir os tanques devem estar completamente vazios de água.
Isso implica que para submergir temos:
Para emergir, o empuxo terá intensidade maior que o Peso do conjunto: