Questão 69352
IFCE
(IFCE - 2012)
A respeito das diagonais de um hexágono regular de Iado medindo 1 cm, é correto afirmar-se que:
são nove, de três comprimentos diferentes, e as menores medem
são nove, de dois comprimentos diferentes, e as maiores medem
são nove, de dois comprimentos diferentes, e as menores medem
são doze, de três comprimentos diferentes, e as maiores medem
são doze, de dois comprimentos diferentes, e as menores medem
Gabarito:
são nove, de dois comprimentos diferentes, e as menores medem
Resolução:
Para responder essa questão é preciso verificar duas coisas: O número de diagonais e a medida delas. Começando pelo número de diagonais:
Para determinar o número de diagonais de um polígono convexo pode ser utilizando a relação:
Em que:
: É o número de diagonais;
:É o número de lados do poligono.
Como o hexágono possui 6 lados deve ser substituído por 6, então têm-se:
Por tanto, o hexágono tem 9 diagonais.
Agora, deve-se analisar a medida dessas diagonais. Para isso, recordemos que um hexágono regular pode ser decomposto em 6 triângulos equiláteros como mostra a figura a baixo:
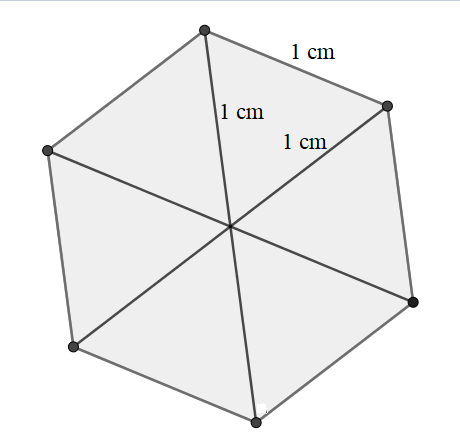
Fonte: Autoria propriá
Escolhendo um vertice para trazar todas diagonais pode ser obtido:
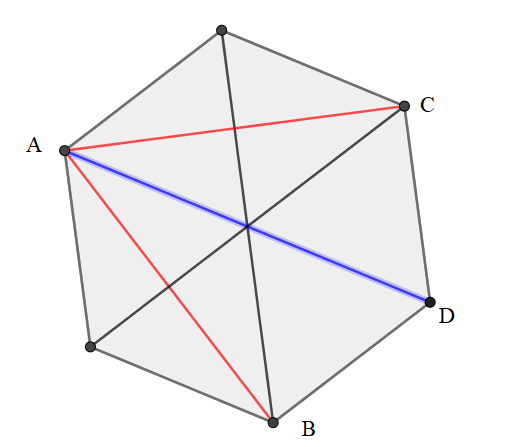
Como o hexágono é regular as diagonais AB e AC (destacadas em vermelho) são iguais e AD corresponde a dois lados do triangulo equilátero então:
Ainda em decorrência do hexágono ser regular as diagonais correspondem a duas alturas dos triângulos equiláteros, ou seja:
Então o hexágono tem diagonais de duas medidas diferentes e as menores medem
Logo, a resposta correta é a Alternativa C