GuruGuia

Questão 77853

ENEM PPL

(ENEM PPL - 2022)

Uma cidade enfrenta racionamento no abastecimento de água. Para minimizar os efeitos da falta de água para seus hóspedes, o gerente de um hotel pretende substituir a caixa-d’água existente por um reservatório. Sabe-se que o consumo médio diário do hotel é de 10 mil litros de água. Mantido o consumo médio diário, o gerente quer que o novo reservatório, uma vez cheio, seja capaz de suprir as necessidades do hotel por, pelo menos, 6 dias completos, mesmo que não haja abastecimento de água nesse período.

O espaço de que o hotel dispõe para instalar o novo reservatório tem formato retangular com largura de 5 m e comprimento de 6 m. O gerente analisa cinco opções disponíveis para esse reservatório.

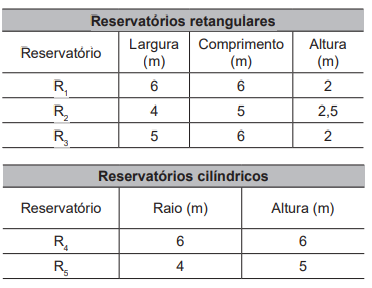
A opção de reservatório que atende à necessidade do hotel e que cabe no espaço disponível é

R₁.

R₂.

R₃.

R₄.

R₅.

Gabarito:

R₃.

Resolução:

A) Incorreta. Inicialmente vamos calcular o espaço disponível:

$A= 5 cdot 6 = 30 m^{2}$

Calculando a área do reservatório R₁: $A_{R_{1}}= 6 cdot 6 = 32 m^{2}$ , vemos que ela ultrapassa o espaço disponível no hotel, logo a altenativa está incorreta.

B) Incorreta. A área de R₂atende ao primeiro critério de espaço, visto que, $A_{R_{2}}= 4 cdot 5 = 20 m^{2}$ . Vamos confirmar se ela também consegue abastecer o hotel por 6 dias consecutivos. Temos:

$V_{R_{2}}= 4 cdot 5 cdot 2,5 = 50 m^{3}$

Contudo, como $10 000 L = 10 m^{3}$ , para abastecer o hotel durante 6 dias precisaremos de $10 m^{3} cdot 6= 60 m^{3}$ , e o reservatório que não atende a essa especificação, visto que ele suporta um volume de apenas 50 m³. Portanto, a alternativa está incorreta.

C) Correta. Inicialmente vamos calcular o espaço disponível:

$A= 5 cdot 6 = 30 m^{2}$

Com base nisso já podemos descartar o reservatório R₁, visto que $A_{R_{1}}= 6 cdot 6 = 32 m^{2}$ sua área ultrapassa o espaço disponível no hotel. Os reservatórios cilíndricos precisam ser descartados, pois deveriam ter um raio da base de no máximo 2,5 m , pois assim poderiam caber dentro de um retângulo de 5 m x 6 m. Como o reservatório R₄ tem raio da base de 6 m e o reservatório R₅ tem raio da base de 4m, então precisamos descartá-los.

Agora, vamos calcular o volume dos reservatórios R₂ e R₃, os únicos que cabem no espaço disponível no hotel. Eles precisam atender à necessidade de suprir o hotel por pelo menos 6 dias completos. Visto que o consumo médio diário do hotel é de 10 000 L de água, temos:

$V_{R_{2}}= 4 cdot 5 cdot 2,5 = 50 m^{3}$

$V_{R_{3}}= 5 cdot 6 cdot 2 = 60 m^{3}$

Como $10 000 L = 10 m^{3}$ , para abastecer o hotel durante 6 dias precisaremos de $10 m^{3} cdot 6= 60 m^{3}$ , e o reservatório que atende a essa especificação é o R_{3 .}

D) Incorreta. Os reservatórios cilíndricos precisam ser descartados, pois deveriam ter um raio da base de no máximo a metade de 5m (pois é a menor medida entre 5 e 6 m), ou seja, os reservartórios cilíndricos deveriam ter raio de no máximo 2,5 m , pois assim poderiam caber dentro de um retângulo de 5 m x 6 m. Como R₄ tem raio da base de 6 m, então precisamos descartá-lo.

E) Incorreta. Os reservatórios cilíndricos precisam ser descartados, pois deveriam ter um raio da base de no máximo a metade de 5m (pois é a menor medida entre 5 e 6 m), ou seja, os reservartórios cilíndricos deveriam ter raio de no máximo 2,5 m , pois assim poderiam caber dentro de um retângulo de 5 m x 6 m. Como R₅ tem raio da base de 4 m, então precisamos descartá-lo.

Questão 1828

ENEM PPL

(Enem PPL 2014) Contam, numa anedota, que certo dia Rui Barbosa saiu às ruas da cidade e se assustou com a quantidade de erros existentes nas placas das casas comerciais e que, diante disso, resolveu instituir um prêmio em dinheiro para o comerciante que tivesse o nome de seu estabelecimento grafado corretamente. Dias depois, Rui Barbosa saiu à procura do vencedor. Satisfeito, encontrou a placa vencedora: “Alfaiataria Águia de Ouro”. No momento da entrega do prêmio, ao dizer o nome da alfaiataria, Rui Barbosa foi interrompido pelo alfaiate premiado, que disse: – Sr. Rui, não é “águia de ouro”; é “aguia de ouro”!

O caráter político do ensino de língua portuguesa no Brasil. Disponível em: http://rosabe.sites.uol.com.br. Acesso em: 2 ago. 2012.

A variação linguística afeta o processo de produção dos sentidos no texto. No relato envolvendo Rui Barbosa, o emprego das marcas de variação objetiva

Ver questão

Questão 1831

ENEM PPL

(ENEM PPL - 2010)

Quando vou a São Paulo, ando na rua ou vou ao mercado, apuro o ouvido; não espero só o sotaque geral dos nordestinos, onipresentes, mas para conferir a pronúncia de cada um; os paulistas pensam que todo nordestino fala igual; contudo as variações são mais numerosas que as notas de uma escala musical. Pernambuco, Paraíba, Rio Grande do Norte, Ceará, Piauí têm no falar de seus nativos muito mais variantes do que se imagina. E a gente se goza uns dos outros, imita o vizinho, e todo mundo ri, porque parece impossível que um praiano de beira-mar não chegue sequer perto de um sertanejo de Quixeramobim. O pessoal do Cariri, então, até se orgulha do falar deles. Têm uns tês doces, quase um the; já nós, ásperos sertanejos, fazemos um duro au ou eu de todos os terminais em al ou el – carnavau, Raqueu... Já os paraibanos trocam o l pelo r. José Américo só me chamava, afetuosamente, de Raquer.

Queiroz, R. O Estado de São Paulo. 09 maio 1998 (fragmento adaptado).

Raquel de Queiroz comenta, em seu texto, um tipo de variação linguística que se percebe no falar de pessoas de diferentes regiões. As características regionais exploradas no texto manifestam-se

Ver questão

Questão 2707

ENEM PPL

(ENEM PPL - 2010)

AMARAL, Tarsila do. O mamoeiro. 1925, óleo sobre tela, 65x70, IEB/USP.

O modernismo brasileiro teve forte influência das vanguardas europeias. A partir da Semana de Arte Moderna, esses conceitos passaram a fazer parte da arte brasileira definitivamente. Tomando como referência o quadro O mamoeiro, identifica-se que nas artes plásticas, a

Ver questão

Questão 3051

ENEM PPL

(Enem PPL 2015)

Ver questão