Questão 53648
UFPR
(UFPR - 2015 - 2ª FASE)
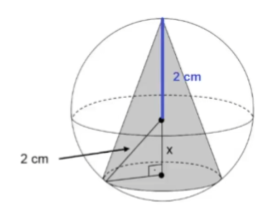
Um cone circular reto está inscrito em uma esfera de raio 2 cm. Indiquemos por x a distância do centro da esfera ao centro da base do cone.
a) Se x = 1 cm, calcule o volume do cone.
b) Calcule o valor de x, sabendo que o volume da esfera é quatro vezes o volume do cone
Gabarito:
Resolução:
a) Olhando para o triângulo apresentado na figura, temos:
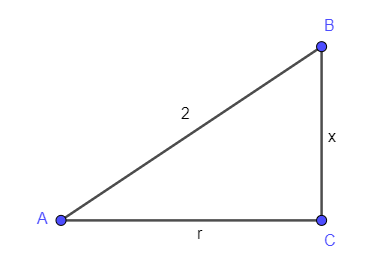
Como no item é dado que x = 1 cm, teremos que:
cm
Além disso, a altura do nosso cone pode ser representada por:
Com isso temos que a altura do cone será 3 cm.
Dessa forma, temos que o volume do cone será:
cm3.
b) Do enunciado da alternativa, temos que:
Onde R é o raio da esfera, r é o raio da base do cone e h a altura do cone. Substituindo R = 2 e simplificando, obtemos:
Olhando para essa figura novamente

Vemos que a altura h será igual a 2 + x e olhando para o triângulo retângulo formado, temos:

Substituindo r2 e h na primeira equação, teremos:
Como temos um produto resultando em zero, temos que ou ou
Resolvendo a segunda igualdade, obtemos:
Dos três possíveis valores de x, vemos que x não pode ser negativo, então temos duas possibilidades ou
(pela representação x = 0 não faz sentido já que x não é um ponto).