Questão 69356

UFMS
  1. Matemática
  2. Matemática

(UFMS - 2018) Em geometria existem muitas simetrias, estudos dos ângulos internos e externos de uma figura. Nesse sentido, um aluno de Matemática desenhou um pentágono regular e, a partir dos seus vértices, traçou todas as diagonais. Assim, verificou a formação de uma estrela de cinco pontas, conforme a figura a seguir:

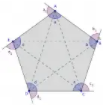
Ao somar os ângulos internos das pontas da estrela, o valor encontrado foi de: 

 

 

A

1.440°.
 

B

540°.

C

180°.
 

D

108°.
 

E

36°.
 

Gabarito:

180°.
 



Resolução:

A soma dos ângulos internos de um polígono regular é dada por:

S_{i} = (n-2) cdot 180 ^{circ}

Portanto, como temos 5 lados:

S_{i} = (5-2) cdot 180 ^{circ} = 540^{circ}

Agora, dividimos a soma dos ângulos pelo número de ângulos para saber quanto vale cada ângulo interno:

a_{i} = frac{540}{5} = 108 ^{circ}

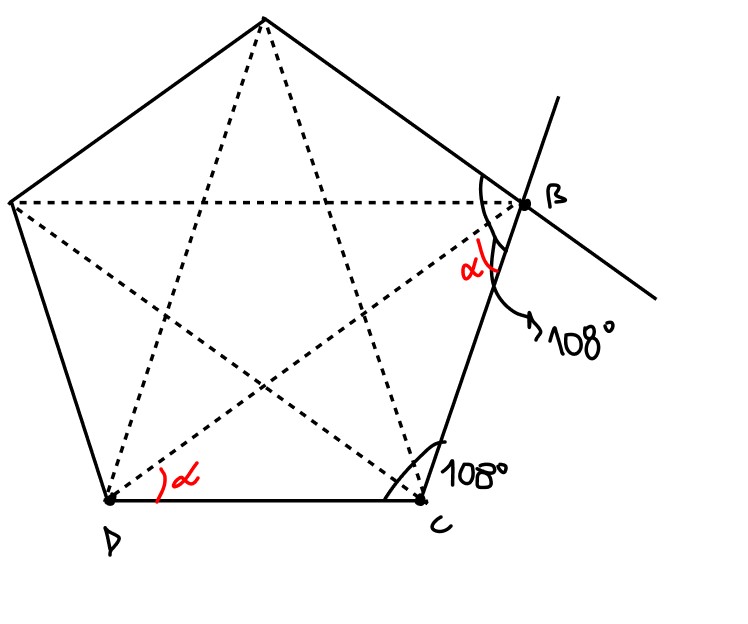
Analisando o triângulo BDC podemos escrever que:

2alpha + 108 = 180

alpha = 36^{circ}

Voltando para o vértice B:

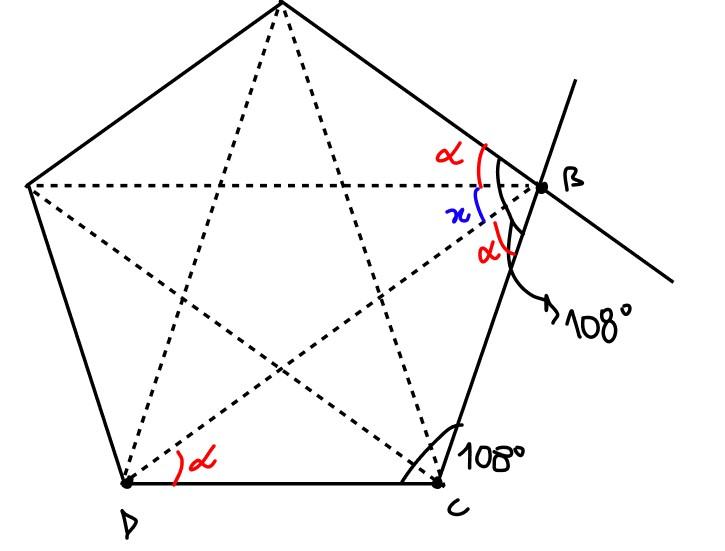
Podemos equacionar que:

2alpha +x = 108

2 cdot 36 +x = 108

x = 108 - 72 = 36 ^{circ}

Como queremos a soma do ângulo x de todas as estrelas:

S_{5} = 5 cdot x = 5 cdot 36 = 180^{circ}



Questão 4111

UFMS
  1. Física
  2. Física

(Ufms 2006) Um carro move-se com velocidade constante de 60 km/h. Começa a chover e o motorista observa que as gotas de água da chuva caem formando um ângulo de 30° com a vertical. Considerando que, em relação à Terra, as gotas caem verticalmente, qual a velocidade em que as gotas de água caem em relação ao carro?

Ver questão

Questão 4141

UFMS
  1. Física
  2. Física

(Ufms 2008) Seja um rio sem curvas e de escoamento sereno sem turbulências, de largura constante igual a L. Considere o escoamento representado por vetores velocidades paralelos às margens e que cresce uniformemente com a distância da margem, atingindo o valor máximo vmáx no meio do rio. A partir daí a velocidade de escoamento diminui uniformemente atingindo o valor nulo nas margens. Isso acontece porque o atrito de escoamento é mais intenso próximo às margens. Um pescador, na tentativa de atravessar esse rio, parte da margem inferior no ponto O com um barco direcionado perpendicularmente às margens e com velocidade constante em relação à água, e igual a u. As linhas pontilhadas, nas figuras, representam possíveis trajetórias descritas pelo barco ao atravessar o rio saindo do ponto O e chegando ao ponto P na margem superior. Com fundamentos nos conceitos da cinemática, assinale a alternativa CORRETA.

Ver questão

Questão 8889

UFMS
  1. Química
  2. Química

(UFMS) Considere o gráfico. Determine a afirmativa correta:

Ver questão

Questão 9131

UFMS
  1. Química
  2. Química

(UFMS)

Numa aula prática de cinética química, um grupo de alunos estudou, nas mesmas condições de temperatura, concentração e pressão, a decomposição do peróxido de hidrogênio, a partir das situações I e II, abaixo descritas:

Situação I: Na presença de íons Fe2+(aq), em meio ácido, em duas etapas:

1ª etapa: H2O2(aq) + 2 Fe2+(aq) + 2 H+(aq)  2 Fe3+(aq) + 2 H2O()

2ª etapa: 2 Fe3+(aq) + H2O2(aq)  2 Fe2+(aq) + O2(g) + 2 H+(aq)

Situação II: Na ausência de íons Fe2+(aq), em meio ácido, em uma única etapa:

2 H2O2(aq)  2 H2O() + O2(g)

A partir da experiência acima descrita, é correto afirmar que:

(01) a velocidade da decomposição do H2O2(aq), em I e II, é a mesma.

(02) os íons Fe2+ se oxidam na 1ª etapa de I, sendo, portanto, oxidantes.

(04) na ausência de íons Fe2+, a decomposição do H2O2(aq) é mais lenta.

(08) na 2ª etapa de I, os íons Fe3+ são oxidantes.

(16) as etapas de I são mais rápidas que a etapa de II.

(32) em I, os íons Fe2+ não são consumidos nas reações.

As afirmativas corretas são:

Ver questão