GuruGuia

Questão 49164

IME

[IME- 2014/2015 - 2ª fase]

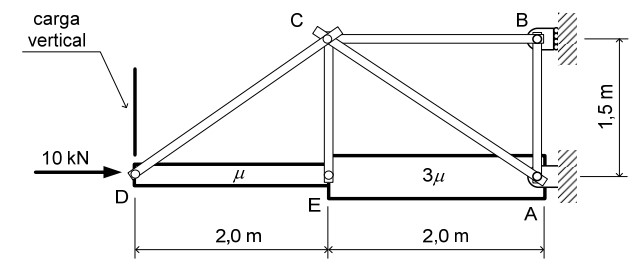
A figura mostra uma estrutura em equilíbrio, formada por barras fixadas por pinos. As barras AE e DE são feitas de um material uniforme e homogêneo. Cada uma das barras restantes tem massa desprezível e seção transversal circular de 16 mm de diâmetro. O apoio B, deformável, é elástico e só apresenta força de reação na horizontal. No ponto D, duas cargas são aplicadas, sendo uma delas conhecida e igual a 10 kN e outra na direção vertical, conforme indicadas na figura. Sabendo que a estrutura no ponto B apresenta um deslocamento horizontal para a esquerda de 2 cm, determine:

a) a magnitude e o sentido da reação do apoio B;

b) as reações horizontal e vertical no apoio A da estrutura, indicando seu sentido;

c) a magnitude e o sentido da carga vertical concentrada no ponto D;

d) o esforço normal (força) por unidade de área da barra BC, indicando sua magnitude e seu tipo (tração ou compressão).

Dados:

• aceleração da gravidade: g = 10 m/s²;

• densidade linear de massa: µ = 100 kg/m;

• constante elástica do apoio B: k = 1600 kN/m.

Gabarito:

Resolução:

Veja a figura:

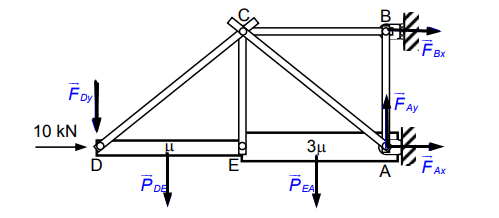a) Considerando que toda a estrutura move-se pra direita no ponto de apoio B, temos uma reação no sentido de reestabelecer a posição de equilíbrio original. Isto posto, a reação de apoio em B será horizontal e pra direita, dada por:

$F_{Bx} = k Delta x$

$F_{Bx} = 1600 cdot 2 cdot 10^{-2} = 32 kN$

b) Para determinar a reação de apoio resultaanete em A, devemos considerar o torque externo do sistema sendo nulo, oriundo da definição de equilíbrio de rotação. O torque resultante em relação a D, é dado por:

$sum {M_{D}} = 0 Rightarrow r_{DE} cdot P_{DE} + r_{EA} cdot P_{EA} + r_{A} cdot F_{A} + r_{B} cdot F_{B} = 0$

Onde r representa o vetor posição das forças, P é o peso das barras, e F_Ae F_Ba reação dos apoios A e B, respectivamente. Assim, decompondo as forças nas direções vertical e horizontal e considerando que a distância da componente horizontal de reação em A, em relação ao ponto D, é nulo, equaciona-se:

$1 P_{DE} + 3 P_{EA} + 1,5 F_{Bx} - 4F_{Ay} = 0$

$1 cdot mu L_{DE} cdot g + 3 cdot 3mu cdot L_{EA} cdot g + 1,5 cdot 32 - 4 F_{Ay} = 0$

$2 + 18 + 48 -4F_{Ay} = 0$

$F_{Ay} = 17 kN$

Como o valor obtido é positivo, o sentido é favorável ao referencial, isto é, pra cima.

Considerando que a resultante das forças horizontais é nula:

$sum {F_{x}} = 0$

$10 + F_{Bx} + F_{Ax} = 0$

$F_{Ax} = -10 -32 = -42 kN$

Portanto, temos uma força na horizontal contrária ao referencial, isto é, para a esquerda.

c) Considerando que a resultante das forças verticais é nula:

$sum {F_{y}} = 0$

$F_{Ay} = P_{DE} + P_{EA} + F_{Dy}$

$F_{Dy} = F_{Ay} - P_{DE} - P_{EA}$

$F_{Dy} = 17 - 2 - 6 = 9 kN$

Considerando que o sentido de $F_{Dy}$ foi assumido como sendo pra baixo e seu valor, calculado acima, é positivo, confirma-se que o sentido da força é pra baixo.

d) Sendo R o raio da barra BC, o esforço da força normal (pressão) pode ser calculado por:

$f_{N} = frac{F_{Bx}}{S}$

$f_{N} = frac{32}{pi R^{2}}$

$f_{N} = frac{32}{pi cdot (8 cdot 10^{-3})^{2}}$

$f_{N} = frac{1 kN}{2pi cdot 10^{-6}} = frac{1000}{2pi cdot 10^{-6}}$

$f_{N} = frac{5}{pi} cdot 10^{8} N/m^{2}$

Questão 992

IME

(IME 2007)

O gráfico acima apresenta a velocidade de um objeto em função do tempo. A aceleração média do objeto no intervalo de tempo de 0 a 4t é:

Ver questão

Questão 993

IME

(IME 2007) Um cubo de material homogêneo, de lado L = 0,4 m e massa M = 40 kg, está preso à extremidade superior de uma mola, cuja outra extremidade está fixada no fundo de um recipiente vazio. O peso do cubo provoca na mola uma deformação de 20 cm. Coloca-se água no recipiente até que o cubo fique com a metade de seu volume submerso. Se a massa específica da água é , a deformação da mola passa a ser:

Ver questão

Questão 994

IME

(IME 2007) Uma nave em órbita circular em torno da Terra usa seus motores para assumir uma nova órbita circular a uma distância menor da superfície do planeta. Considerando desprezível a variação da massa do foguete, na nova órbita:

Ver questão

Questão 995

IME

(IME 2007) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderá ser nula se, dentre as opções abaixo, a transformação seguinte for uma:

Ver questão