GuruGuia

Questão 33391

IME

[IME- 2014/2015 - 2ª fase]

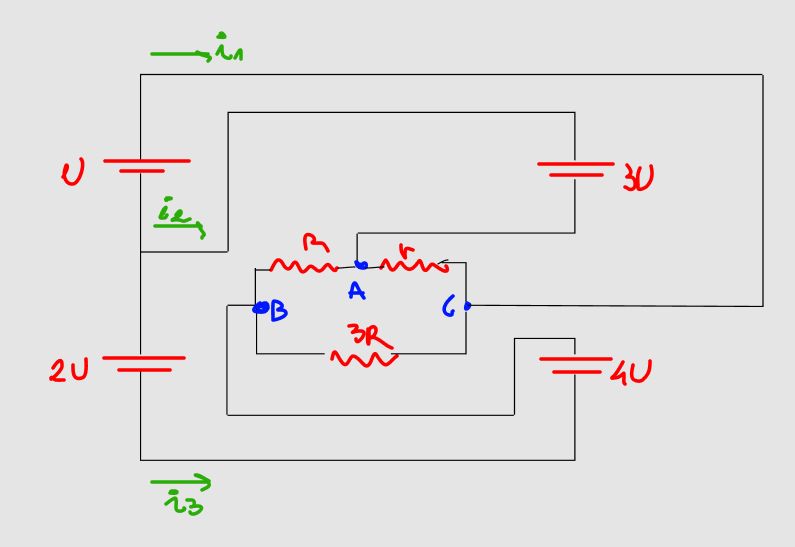
A figura acima apresenta um circuito composto por quatro baterias e três resistores. Sabendo-se que l₁ é igual a $10frac{U}{R}$ determine, em função de U e R

a) a resistência r

b) o somatório de l₁, l₂ e l_3;

c) a potência total dissipada pelos resistores;

d) a energia consumida pelo resistor 3R em 30 minutos.

Gabarito:

Resolução:

De A para B temos os potenciais:

$V_{A} + 3U - 2U + 4U = V_{B}$

Portanto, a ddp será:

$V_{B} - V_{A} = 5U$

De para C, temos os potenciais:

$V_{A} + 3U + U = V_{C}$

Analogamente:

$V_{C} - V_{A} = 4U$

Do ponto B para C:

$V_{B} - 4U + 2U + U = V_{C}$

$V_{B} - V_{C} = U$

Como a corrente se desloca do maior para o menor potencial, temos os sentidos das correntes em cada resistor indicados pelo seguinte diagrama:

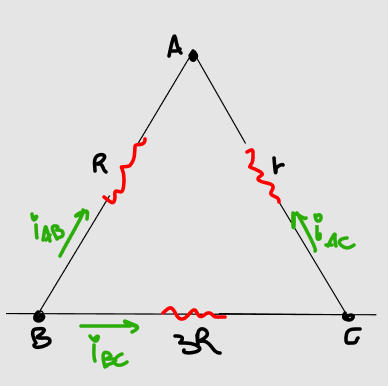Portanto, pela Primeira Lei de Ohm:

$i_{AB} = frac{V_{B} - V_{A}}{R} = frac{5U}{R}$

$i_{AC} = frac{V_{C} - V_{A}}{r} = frac{4U}{r}$

$i_{BC} = frac{V_{B} - V_{C}}{3R} = frac{U}{3R}$

a) Aplicando a lei dos nós no ponto C:

$i_{AC} = i_{BC} + I_{1}$

$frac{4U}{r} = frac{U}{3R} + frac{10U}{R}$

$frac{4}{r} = frac{1+30}{3R}$

$r = frac{12}{31} R$

b) No ponto D:

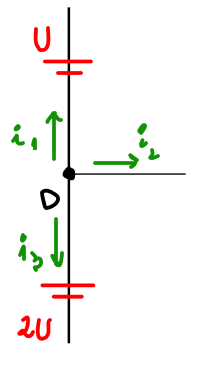
Aplicando a lei dos nós, percebemos que não há corrente chegando em D, portanto:

$i_{1} + i_{2} + i_{3} = 0$

Naturalmente, pelo menos uma dessas correntes deve ter sentido contrário àquele adotado pelo diagrama da figura.

c) A potência total dissipada corresponde a soma das potências dissipadas por cada resistor individualmente:

$P = frac{(V_{B} - V_{A})^{2}}{R} + frac{(V_{C} - V_{A})^{2}}{r} + frac{(V_{B} - V_{C})^{2}}{3R}$

$P = frac{(5U)^{2}}{R} + frac{(4U)^{2}}{frac{12}{31} R} + frac{U^{2}}{3R}$

$P = frac{200 U^{2}}{3R}$

d) Sendo P₃a potência dissipada e E a energia consumida pelo resistor 3R em 30 minutos (1800 segundos) temos que:

$P_{3} = frac{E}{Delta t}$

$frac{U^{2}}{3R} = frac{E}{1800}$

$E = frac{600U^{2}}{R}$

Questão 992

IME

(IME 2007)

O gráfico acima apresenta a velocidade de um objeto em função do tempo. A aceleração média do objeto no intervalo de tempo de 0 a 4t é:

Ver questão

Questão 993

IME

(IME 2007) Um cubo de material homogêneo, de lado L = 0,4 m e massa M = 40 kg, está preso à extremidade superior de uma mola, cuja outra extremidade está fixada no fundo de um recipiente vazio. O peso do cubo provoca na mola uma deformação de 20 cm. Coloca-se água no recipiente até que o cubo fique com a metade de seu volume submerso. Se a massa específica da água é , a deformação da mola passa a ser:

Ver questão

Questão 994

IME

(IME 2007) Uma nave em órbita circular em torno da Terra usa seus motores para assumir uma nova órbita circular a uma distância menor da superfície do planeta. Considerando desprezível a variação da massa do foguete, na nova órbita:

Ver questão

Questão 995

IME

(IME 2007) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderá ser nula se, dentre as opções abaixo, a transformação seguinte for uma:

Ver questão