GuruGuia

Questão 49160

IME

[IME- 2014/2015 - 2ª fase]

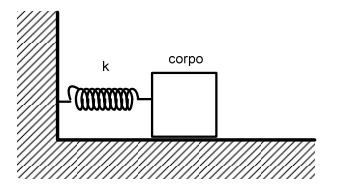
Um corpo com massa m, inicialmente em repouso sobre uma superfície horizontal e preso a uma mola de constante elástica k, representado na figura, recebe um impulso I, para a direita, dando início a um Movimento Harmônico Simples (MHS). Inicialmente não existe atrito entre o corpo e a superfície horizontal devido à presença de um lubrificante. Contudo, após 1000 ciclos do MHS, o lubrificante perde eficiência e passa a existir atrito constante entre o corpo e a superfície horizontal. Diante do exposto, determine:

a) a máxima amplitude de oscilação;

b) o módulo da aceleração máxima;

c) a máxima energia potencial elástica;

d) a distância total percorrida pelo corpo até que este pare definitivamente.

Dados:

• massa do corpo: m = 2 kg;

• impulso aplicado ao corpo: I = 4 kg.m/s;

• constante elástica da mola: k = 8 N/m;

• coeficiente de atrito: µ = 0,1;

• aceleração da gravidade: g = 10 m/s².

Observação:

• a massa da mola é desprezível em relação à massa do corpo.

Gabarito:

Resolução:

a) O impulso é calculado por: $I = mv$

$v = frac{l}{m}$

Pela conservação de energia:

$frac{mv^{2}}{2} = frac{kA^{2}}{2}$

$A^{2} = frac{mv^{2}}{k} = frac{m (frac{l}{m})^{2}}{k}$

Substituindo os valores A = 1 m

b) É necessário analisar a situação com e sem atrito. Para o caso do atrito ser desprezível a aceleração máxima ocorre em x = 1 metro. Portanto:

$a = frac{kx}{m} = frac{8}{2} = 4 m/s^{2}$

Com atrito, primeiro devemos encontrar a elongação máxima.

Ainda, pela conservação de energia:

$E_{total} = E_{el} + | W_{atrito} |$

$E_{total} = frac{kd^{2}}{2} + mgmu d$

Substituindo os valores:

$4 = 4d^{2} + 2d$

$2d^{2} + d -2 = 0$

Resolvendo por Bhaskara e mantendo a raiz conveniente:

$d = frac{-1 + sqrt{17}}{4}$

Quando x = d teremos a aceleração máxima e a força resultante será dada por:

$R = F_{el} + F_{at}$

$ma_{max} = kd + mgmu$

$2 a_{max} = 8 cdot frac{(sqrt{17} -1)}{4} + 2$

$a_{max} = sqrt{17} m/s^{2}$

c) A energia potencial elástica máxima ocorre quando x = A, na situação sem atrito:

$E_{el} = frac{kx^{2}}{2} = frac{8}{2} = 4 J$

d) O sistema entrará em repouso quando a resultante das forças for zero e sua veloidade também. Como vimos que são realizados 1000 ciclos, o atrito passa a atuar quando o bloco passa pelo ponto de amplitude nula, atingindo uma máxima amplitude a uma distância d já calculada.

Neste ponto, a força de atrito tem seu módulo máximo, tal que:

$F_{el} = kd$

$F_{el} = 8 cdot frac{-1 + sqrt{17}}{4}$

$F_{el} = -2 + sqrt{17} > -2 +4 = F_{at}$

Assim, temos a condição de velocidade nula, mas não da resultante nula das forças. Portanto, vamos analisar a nova posição em que a velocidade se anula:

$E_{total} = E_{el} + |W_{Atrito}|$

$frac{kd^{2}}{2} = frac{kx_{1}^{2}}{2} + mg mu (d-x_{1})$

Temos uma equação de segundo grau na qual sabemos pelo menos uma das raizes, isto é, igual a d.

$x_{1} = d = frac{-1 + sqrt{17}}{4}$

Assim, podemos encontrar a outra equação por soma e produto:

$kx_{1}^{2} - 2mg mu x_{1} + d (2mgmu - kd) = 0$

$S = frac{2mgmu}{k} = frac{-1 + sqrt{17}}{4} + x_1$

$frac{2 cdot 2}{8} = frac{-1 + sqrt{17}}{4} + x_{1} '$

$x_{1} ' = frac{3 - sqrt{17}}{4} m$

Obtendo a força elástica para verificar se satisfaz o equilíbrio, obtemos:

$F_{el} = 2 cdot |3 - sqrt{17} | > 2 cdot |3-4| = F_{at}$

Dessa maneira, o corpo ainda não se encontrará em equilíbrio estático, mais uma vez, temos:

$E_{total} = E_{el} + |W_{atrito} | Leftrightarrow frac{kx_{1}^{2}}{2} = frac{kx_{2}}{2} + mgmu (x_{2} - x_{1})$

Montando a equação:

$kx_{2}^{2} + 2mg mu x_{2} - x_{1} (2mgmu + kx_{1}) = 0$

Analogamente, por soma e produto:

$S = - frac{2mg mu}{k} = frac{3 - sqrt{17}}{4} + x_{2}$

$frac{2 cdot 2}{8} = frac{3 - sqrt{17}}{4} + x_{2} '$

$x_{2} ' = frac{-5 + sqrt{17}}{4} m$

Verificando se a condição é satisfeita:

$F_{el} = 2 cdot | -5 + sqrt{17} | < 2 cdot | -5 + 4 | = F_{at}$

Como queremos a distância percorrida, temos que somar as distâncias percorridas durante as oscilações isentas de atrito mais aquelas enquanto atua a força de atrito.

$D = 4000 + 2 |d| + 2 |x_{1} '| - |x_{2}|$

$D = (4000 + frac{5 sqrt{17} - 13}{4}) m$

Questão 992

IME

(IME 2007)

O gráfico acima apresenta a velocidade de um objeto em função do tempo. A aceleração média do objeto no intervalo de tempo de 0 a 4t é:

Ver questão

Questão 993

IME

(IME 2007) Um cubo de material homogêneo, de lado L = 0,4 m e massa M = 40 kg, está preso à extremidade superior de uma mola, cuja outra extremidade está fixada no fundo de um recipiente vazio. O peso do cubo provoca na mola uma deformação de 20 cm. Coloca-se água no recipiente até que o cubo fique com a metade de seu volume submerso. Se a massa específica da água é , a deformação da mola passa a ser:

Ver questão

Questão 994

IME

(IME 2007) Uma nave em órbita circular em torno da Terra usa seus motores para assumir uma nova órbita circular a uma distância menor da superfície do planeta. Considerando desprezível a variação da massa do foguete, na nova órbita:

Ver questão

Questão 995

IME

(IME 2007) Um gás ideal sofre uma expansão isotérmica, seguida de uma compressão adiabática. A variação total da energia interna do gás poderá ser nula se, dentre as opções abaixo, a transformação seguinte for uma:

Ver questão