Questão 49158
IME
[IME- 2014/2015 - 2ª fase]
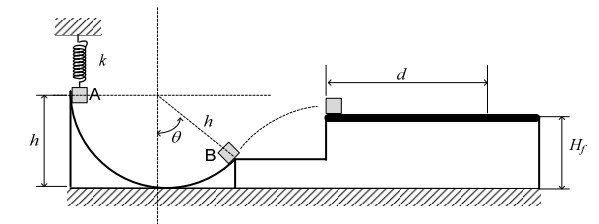
Uma mola comprimida por uma deformação x está em contato com um corpo de massa m, que se encontra inicialmente em repouso no Ponto A da rampa circular. O corpo é liberado e inicia um movimento sem atrito na rampa. Ao atingir o ponto B sob um ângulo θ indicado na figura, o corpo abandona a superfície da rampa. No ponto mais alto da trajetória, entra em contato com uma superfície plana horizontal com coeficiente de atrito cinético µ. Após deslocar-se por uma distância d nesta superfície horizontal, o corpo atinge o repouso. Determine, em função dos parâmetros mencionados:
a) a altura final do corpo Hf em relação ao solo;
b) a distância d percorrida ao longo da superfície plana horizontal.
Dados:
• aceleração da gravidade: g;
• constante elástica da mola: k;
• raio da rampa circular: h.
Gabarito:
Resolução:
a) Por conservação da energia mecânica, considerando a parte mais baixa da rampa circular como local de energia potencial nula:
Há duas incógnitas: a velocidade e Hf. Mas, pela figura do enunciado:
Em que delta H é a altura a partir do ponto de lançamento que o corpo atinge. Obtemos ela por:
Isolando em (I):
Substituindo (III) em (II):
b) Como :