Enem/2020
Questão 66894
ENEM DIGITAL
(ENEM DIGITAL - 2020)
Em um ano, uma prefeitura apresentou o relatório de gastos públicos realizados pelo município. O documento mostra que foram gastos 72 mil reais no mês de janeiro (mês 1), que o maior gasto mensal ocorreu no mês de agosto (mês 8) e que a prefeitura gastou 105 mil reais no mês de dezembro (mês 12). A curva que modela esses gastos é a parábola y = T(x), com x sendo o número correspondente ao mês e T(x), em milhar de real.
A expressão da função cujo gráfico é o da parábola descrita é
Ver questão
Questão 66895
ENEM DIGITAL
(ENEM DIGITAL - 2020)
Um marceneiro visitou 5 madeireiras para comprar tábuas que lhe permitissem construir 5 prateleiras de formato retangular, de dimensões iguais a 30 cm de largura por 120 cm de comprimento cada, tendo como objetivo minimizar a sobra de madeira, podendo, para isso, fazer qualquer tipo de emenda. As dimensões das tábuas encontradas nas madeireiras estão descritas no quadro.
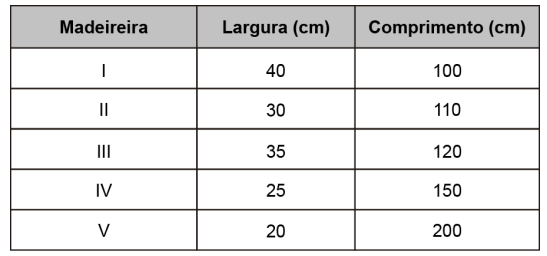
Em qual madeireira o marceneiro deve comprar as tábuas para atingir seu objetivo?
Ver questãoQuestão 66896
ENEM DIGITAL
(ENEM DIGITAL - 2020)
“1, 2, 3, GOL, 5, 6, 7, GOL, 9, 10, 11, GOL, 13, GOL, 15, GOL, 17, 18, 19, GOL, 21, 22, 23, GOL, 25, ...”
Para a Copa do Mundo de Futebol de 2014, um bar onde se reuniam amigos para assistir aos jogos criou uma brincadeira. Um dos presentes era escolhido e tinha que dizer, numa sequência em ordem crescente, os números naturais não nulos, trocando os múltiplos de 4 e os números terminados em 4 pela palavra GOL. A brincadeira acabava quando o participante errava um termo da sequência.
Um dos participantes conseguiu falar até o número 103, respeitando as regras da brincadeira.
O total de vezes em que esse participante disse a palavra GOL foi
Ver questãoQuestão 66897
ENEM DIGITAL
(ENEM DIGITAL - 2020)
Na última eleição para a presidência de um clube, duas chapas se inscreveram (I e II). Há dois tipos de sócio: patrimoniais e contribuintes. Votos de sócios patrimoniais têm peso 0,6 e de sócios contribuintes têm peso 0,4. A chapa I recebeu 850 votos de sócios patrimoniais e 4 300 de sócios contribuintes; a chapa II recebeu 1 300 votos de sócios patrimoniais e 2 120 de sócios contribuintes. Não houve abstenções, votos em branco ou nulos, e a chapa I foi vencedora. Haverá uma nova eleição para a presidência do clube, com o mesmo número e tipos de sócios, e as mesmas chapas da eleição anterior. Uma consulta feita pela chapa II mostrou que os sócios patrimoniais não mudarão seus votos, e que pode contar com os votos dos sócios contribuintes da última eleição. Assim, para que vença, será necessária uma campanha junto aos sócios contribuintes com o objetivo de que mudem seus votos para a chapa II.
A menor quantidade de sócios contribuintes que precisam trocar seu voto da chapa I para a chapa II para que esta seja vencedora é
Ver questãoQuestão 66898
ENEM DIGITAL
(ENEM DIGITAL - 2020)
Uma microempresa especializou-se em produzir um tipo de chaveiro personalizado para brindes. O custo de produção de cada unidade é de R$ 0,42 e são comercializados em pacotes com 400 chaveiros, que são vendidos por R$ 280,00. Além disso, essa empresa tem um custo mensal fixo de R$ 12 800,00 que não depende do número de chaveiros produzidos.
Qual é o número mínimo de pacotes de chaveiros que devem ser vendidos mensalmente para que essa microempresa não tenha prejuízo no mês?
Ver questãoQuestão 66899
ENEM DIGITAL
(ENEM DIGITAL - 2020)
Um investidor deseja aplicar R$ 10 000,00 durante um mês em um dos fundos de investimento de um banco. O agente de investimentos desse banco apresentou dois tipos de aplicações financeiras: a aplicação Básica e a aplicação Pessoal, cujas informações de rendimentos e descontos de taxas administrativas mensais são apresentadas no quadro.
| Aplicação | Taxa de Rendimento Mensal | Taxa Administrativa mensal |
|---|---|---|
| Básica | 0,542% | R$ 0,30 |
| Pessoal | 0,560% | 3,8% sobre o rendimento mensal |
Consideradas as taxas de rendimento e administrativa, qual aplicação fornecerá maior valor de rendimento líquido a esse investidor e qual será esse valor?
Ver questão
Questão 66900
ENEM DIGITAL
(ENEM DIGITAL - 2020)
Por muitos anos, o Brasil tem figurado no cenário mundial entre os maiores produtores e exportadores de soja. Entre os anos de 2010 e 2014, houve uma forte tendência de aumento da produtividade, porém, um aspecto dificultou esse avanço: o alto custo do imposto ao produtor associado ao baixo preço de venda do produto. Em média, um produtor gastava R$ 1 200,00 por hectare plantado, e vendia por R$ 50,00 cada saca de 60 kg. Ciente desses valores, um produtor pode, em certo ano, determinar uma relação do lucro L que obteve em função das sacas de 60 kg vendidas. Suponha que ele plantou 10 hectares de soja em sua propriedade, na qual colheu x sacas de 60 kg e todas as sacas foram vendidas.
Disponível em: www.cnpso.embrapa.br. Acesso em: 27 fev. 2012 (adaptado).
Qual é a expressão que determinou o lucro L em função de x obtido por esse produtor nesse ano?
Ver questãoQuestão 66901
ENEM DIGITAL
(ENEM DIGITAL - 2020)
Os tempos gastos por três alunos para resolver um mesmo exercício de matemática foram: 3,25 minutos; 3,4 minutos e 191 segundos.
O tempo gasto a mais, em segundo, pelo aluno que concluiu por último a resolução do exercício, em relação ao primeiro que o finalizou, foi igual a
Ver questãoQuestão 66902
ENEM DIGITAL
(ENEM DIGITAL - 2020)
Uma empresa de chocolates consultou o gerente de produção e verificou que existem cinco tipos diferentes de barras de chocolate que podem ser produzidas, com os seguintes preços no mercado:
• Barra I: R$ 2,00;
• Barra II: R$ 3,50;
• Barra III: R$ 4,00;
• Barra IV: R$ 7,00;
• Barra V: R$ 8,00.
Analisando as tendências do mercado, que incluem a quantidade vendida e a procura pelos consumidores, o gerente de vendas da empresa verificou que o lucro L com a venda de barras de chocolate é expresso pela função L(x) = – x2 + 14x – 45, em que x representa o preço da barra de chocolate.
A empresa decide investir na fabricação da barra de chocolate cujo preço praticado no mercado renderá o maior lucro.
Nessas condições, a empresa deverá investir na produção da barra
Questão 66904
ENEM DIGITAL
(ENEM DIGITAL - 2020)
A figura ilustra a vista superior de um brinquedo gira-gira em um parque de diversões, no qual a linha contínua, em formato circular tendo O como seu centro, indica o assento onde as crianças se posicionam no brinquedo. O ponto P indica a posição ocupada por uma criança, em um instante de tempo T, quando o brinquedo está girando continuamente no sentido anti-horário (com O fixo), e velocidade constante por várias voltas.
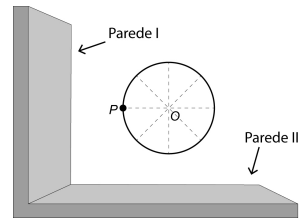
O brinquedo está situado nas proximidades de duas paredes verticais e perpendiculares entre si. Seja D a distância de P até a parede I.
O gráfico que melhor representa, em função do tempo t a partir do instante T, a distância D é
Ver questão