Enem/2023

Questão 81742

(ENEM - 2023)

Visando atrair mais clientes, o gerente de uma loja anunciou uma promoção em que cada cliente que realizar uma compra pode ganhar um voucher para ser usado em sua próxima compra. Para ganhar seu voucher, o cliente precisa retirar, ao acaso, uma bolinha de dentro de cada uma das duas urnas A e B disponibilizadas pelo gerente, nas quais há apenas bolinhas pretas e brancas. Atualmente, a probabilidade de se escolher, ao acaso, uma bolinha preta na urna A é igual a 20% e a probabilidade de se escolher uma bolinha preta na urna B é 25%. Ganha o voucher o cliente que retirar duas bolinhas pretas, uma de cada urna.

Com o passar dos dias, o gerente percebeu que, para a promoção ser viável aos negócios, era preciso alterar a probabilidade de acerto do cliente sem alterar a regra da promoção. Para isso, resolveu alterar a quantidade de bolinhas brancas na urna B de forma que a probabilidade de um cliente ganhar o voucher passasse a ser menor ou igual a 1%. Sabe-se que a urna B tem 4 bolinhas pretas e que, em ambas as urnas, todas as bolinhas têm a mesma probabilidade de serem retiradas.

Qual é o número mínimo de bolinhas brancas que o gerente deve adicionar à urna B?

Questão 81743

(ENEM - 2023)

O gerente de uma fábrica pretende comparar a evolução das vendas de dois produtos similares (I e II). Para isso, passou a verificar o número de unidades vendidas de cada um desses produtos em cada mês. Os resultados dessa verificação, para os meses de abril a junho, são apresentados na tabela.

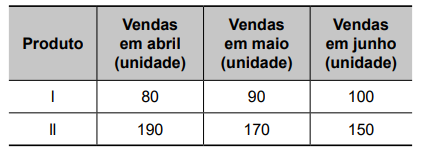
O gerente estava decidido a cessar a produção do produto II no mês seguinte àquele em que as vendas do produto I superassem as do produto II.

Suponha que a variação na quantidade de unidades vendidas dos produtos I e II se manteve, mês a mês, como no período representado na tabela.

Em qual mês o produto II parou de ser produzido?

Questão 81744

(ENEM - 2023)

Uma empresa de transporte faz regularmente um levantamento do número de viagens realizadas durante o dia por todos os 160 motoristas cadastrados em seu aplicativo. Em um certo dia, foi gerado um relatório, por meio de um gráfico de barras, no qual se relacionaram a quantidade de motoristas com a quantidade de viagens realizadas até aquele instante do dia.

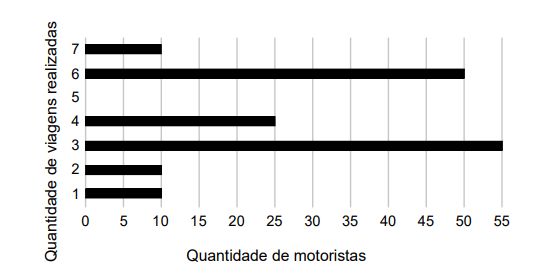
Comparando os valores da média, da mediana e da moda da distribuição das quantidades de viagens realizadas pelos motoristas cadastrados nessa empresa, obtém-se

Questão 81745

(ENEM - 2023)

No alojamento de uma universidade, há alguns quartos com o padrão superior ao dos demais. Um desses quartos ficou disponível, e muitos estudantes se candidataram para morar no local. Para escolher quem ficará com o quarto, um sorteio será realizado. Para esse sorteio, cartões individuais com os nomes de todos os estudantes inscritos serão depositados em uma urna, sendo que, para cada estudante de primeiro ano, será depositado um único cartão com seu nome; para cada estudante de segundo ano, dois cartões com seu nome; e, para cada estudante de terceiro ano, três cartões com seu nome. Foram inscritos 200 estudantes de primeiro ano, 150 de segundo ano e 100 de terceiro ano. Todos os cartões têm a mesma probabilidade de serem sorteados.

Qual a probabilidade de o vencedor do sorteio ser um estudante de terceiro ano?

Questão 81746

(ENEM - 2023)

A água utilizada pelos 75 moradores de um vilarejo provém de um reservatório de formato cilíndrico circular reto cujo raio da base mede 5 metros, sempre abastecido no primeiro dia de cada mês por caminhões-pipa. Cada morador desse vilarejo consome, em média, 200 litros de água por dia.

No mês de junho de um determinado ano, o vilarejo festejou o dia do seu padroeiro e houve um gasto extra de água nos primeiros 20 dias. Passado esse período, as pessoas verificaram a quantidade de água presente no reservatório e constataram que o nível da coluna de água estava em 1,5 metro. Decidiram, então, fazer um racionamento de água durante os 10 dias seguintes. Considere 3 como aproximação para .

Qual é a quantidade mínima de água, em litro, que cada morador, em média, deverá economizar por dia, de modo que o reservatório não fique sem água nos próximos 10 dias?

Questão 81747

(ENEM - 2023)

Em janeiro do ano passado, a direção de uma fábrica abriu uma creche para os filhos de seus funcionários, com 10 salas, cada uma com capacidade para atender 10 crianças a cada ano. As vagas são sorteadas entre os filhos dos funcionários inscritos, enquanto os não contemplados pelo sorteio formam uma lista de espera. No ano passado, a lista de espera teve 400 nomes e, neste ano, esse número cresceu 10%.

A direção da fábrica realizou uma pesquisa e constatou que a lista de espera para o próximo ano terá a mesma quantidade de nomes da lista de espera deste ano. Decidiu, então, construir, ao longo desse ano, novas salas para a creche, também com capacidade de atendimento para 10 crianças cada, de modo que o número de nomes na lista de espera no próximo ano seja 25% menor que o deste ano.

O número mínimo de salas que deverão ser construídas é

Questão 81748

(ENEM - 2023)

A foto mostra a construção de uma cisterna destinada ao armazenamento de água. Uma cisterna como essa, na forma de cilindro circular reto com 3 m² de área da base, foi abastecida por um curso-d’água com vazão constante. O seu proprietário registrou a altura do nível da água no interior da cisterna durante o abastecimento em diferentes momentos de um mesmo dia, conforme o quadro.

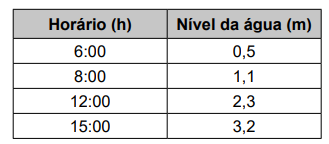
Qual foi a vazão, em metro cúbico por hora, do curso-d’água que abasteceu a cisterna?

Questão 81749

(ENEM - 2023)

Num certo momento de um jogo digital, a tela apresenta a imagem representada na figura. O ponto Q₁ representa a posição de um jogador que está com a bola, os pontos Q₂, Q₃, Q₄ , Q₅ e Q₆ também indicam posições de jogadores da mesma equipe, e os pontos A e B indicam os dois pés da trave mais próxima deles. No momento da partida retratado, o jogador Q₁ tem a posse da bola, que será passada para um dos outros jogadores das posições Q_n, n ∈ {2, 3, 4, 5, 6}, cujo ângulo tenha a mesma medida do ângulo .

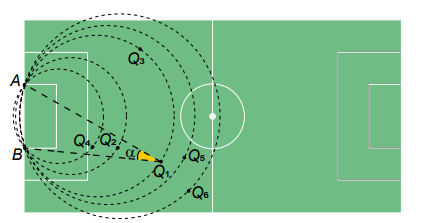
Qual é o jogador que receberá a bola?

Questão 81750

(ENEM - 2023)

O triângulo da figura é denominado triângulo mágico. Nos círculos, escrevem-se os números de 1 a 6, sem repetição, com um número em cada círculo. O objetivo é distribuir os números de forma que as somas dos números em cada lado do triângulo sejam iguais.

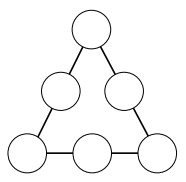
Considere que os números colocados nos vértices do triângulo estejam em progressão aritmética de razão igual a 2.

Nas condições propostas, quais as possíveis soluções para as somas dos números que formam os lados do triângulo?

Questão 81751

(ENEM - 2023)

Alguns estudos comprovam que os carboidratos fornecem energia ao corpo, preservam as proteínas estruturais dos músculos durante a prática de atividade física e ainda dão força para o cérebro coordenar os movimentos, o que de fato tem impacto positivo no desenvolvimento do praticante. O ideal é consumir 1 grama de carboidrato para cada minuto de caminhada.

CIRINO, C. Boa pergunta: consumir carboidratos antes dos exercícios melhora o desempenho do atleta? Revista Saúde! É Vital, n. 330, nov. 2010 (adaptado).

Um casal realizará diariamente 30 minutos de caminhada, ingerindo, antes dessa atividade, a quantidade ideal de carboidratos recomendada. Para ter o consumo ideal apenas por meio do consumo de pão de fôrma integral, o casal planeja garantir o suprimento de pães para um período de 30 dias ininterruptos.Sabe-se que cada pacote desse pão vem com 18 fatias, e que cada uma delas tem 15 gramas de carboidratos.

A quantidade mínima de pacotes de pão de fôrma necessários para prover o suprimento a esse casal é