FUVEST 2006
Questão 51637
UNICAMP
(UNICAMP - 2006 - 2 FASE ) Um brinquedo que muito agrada às crianças são os lançadores de objetos em uma pista. Considere que a mola da figura abaixo possui uma constante elástica k = 8000 N/m e massa desprezível. Inicialmente, a mola está comprimida de 2,0 cm e, ao ser liberada, empurra um carrinho de massa igual a 0,20 kg. O carrinho abandona a mola quando esta atinge o seu comprimento relaxado, e percorre uma pista que termina em uma rampa. Considere que não há perda de energia mecânica por atrito no movimento do carrinho.
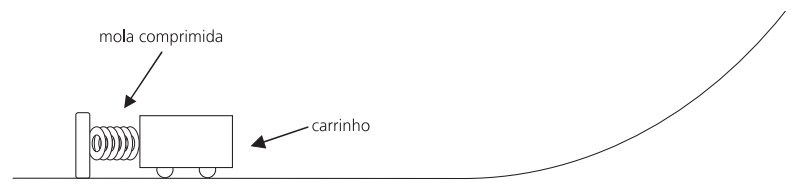
a) Qual é a velocidade do carrinho quando ele abandona a mola?
b) Na subida da rampa, a que altura o carrinho tem velocidade de 2,0 m/s?
Questão 51638
UNICAMP
(UNICAMP - 2006 - 2 FASE ) Ao se usar um saca-rolhas, a força mínima que deve ser aplicada para que a rolha de uma garrafa comece a sair é igual a 360 N.
a) Sendo µe = 0,2 o coeficiente de atrito estático entre a rolha e o bocal da garrafa, encontre a força normal que a rolha exerce no bocal da garrafa. Despreze o peso da rolha.
b) Calcule a pressão da rolha sobre o bocal da garrafa. Considere o raio interno do bocal da garrafa igual a 0,75 cm e o comprimento da rolha igual a 4,0 cm.
Questão 51639
UNICAMP
(UNICAMP - 2006 - 2 FASE ) Em uma auto-estrada, por causa da quebra de uma ponta de eixo, a roda de um caminhão desprende-se e vai em direção à outra pista, atingindo um carro que vem em sentido oposto. A roda é lançada com uma velocidade de 72 km/h, formando um ângulo de 30º com a pista, como indicado na figura abaixo. A velocidade do carro antes da colisão é de 90 km/h; a massa do carro é igual a 900 kg e a massa da roda do caminhão é igual a 100 kg. A roda fica presa ao carro após a colisão.
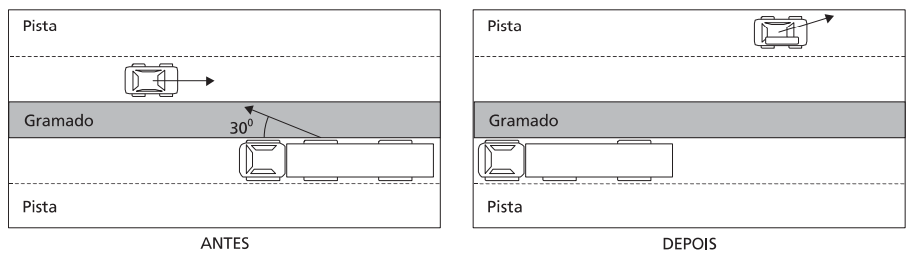
a) Imediatamente após a colisão, qual é a componente da velocidade do carro na direção transversal à pista?
b) Qual é a energia cinética do conjunto carro-roda imediatamente após a colisão?
Se for necessário, use: sen 30º = 0,5, cos 30º = 0,87.
Questão 51640
UNICAMP
(UNICAMP - 2006 - 2 FASE ) Um pêndulo cônico é formado por um fio de massa desprezível e comprimento L = 1,25 m, que suporta uma massa m = 0,5 kg na sua extremidade inferior. A extremidade superior do fio é presa ao teto, conforme ilustra a fi gura abaixo. Quando o pêndulo oscila, a massa m executa um movimento circular uniforme num plano horizontal, e o ângulo que o fi o forma com a vertical é = 60º
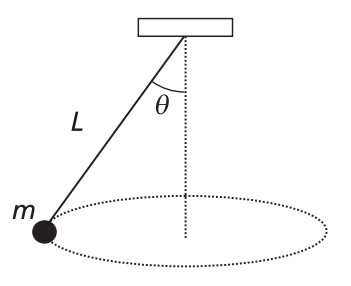
a) Qual é a tensão no fio?
b) Qual é a velocidade angular da massa?
Se for necessário, use: sen 60º = 0,87, cos 60º = 0,5.
Questão 51641
UNICAMP
(UNICAMP - 2006 - 2 FASE ) Todos os corpos trocam energia com seu ambiente através da emissão e da absorção de ondas eletromagnéticas em todas as frequências. Um corpo negro é um corpo que absorve toda onda eletromagnética nele incidente, sendo que também apresenta a máxima eficiência de emissão. A intensidade das ondas emitidas por um corpo negro só depende da temperatura desse corpo. O corpo humano à temperatura normal de 37 ºC pode ser considerado como um corpo negro. Considere que a velocidade das ondas eletromagnéticas é igual a 3,0×108 m/s.
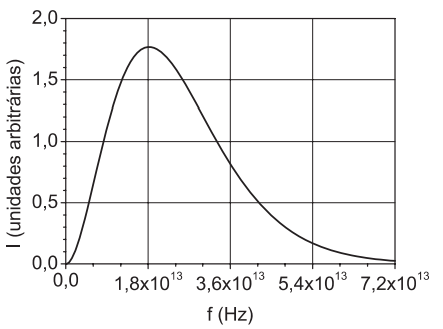
a) A fi gura abaixo mostra a intensidade das ondas eletromagnéticas emitidas por um corpo negro a 37 ºC em função da frequência. Qual é o comprimento de onda correspondente à frequência para a qual a intensidade é máxima?
b) Se um corpo negro cuja temperatura absoluta é T se encontra num ambiente cuja temperatura absoluta é Ta, a potência líquida que ele perde por emissão e absorção de ondas eletromagnéticas é dada por , onde A é a área da superfície do corpo e
= 6 × 10-8 W/(m2K4). Usando como referência uma pessoa com 1,70 m de altura e 70 kg de massa, faça uma estimativa da área da superfície do corpo humano. A partir da área estimada, calcule a perda total diária de energia por emissão e absorção de ondas eletromagnéticas por essa pessoa se ela se encontra num ambiente a 27 ºC. Aproxime a duração de 1 dia por 9,0 × 104 s.
Questão 51642
UNICAMP
(UNICAMP - 2006 - 2 FASE ) Desconfiada de que o anel que ganhara do namorado não era uma liga de ouro de boa qualidade, uma estudante resolveu tirar a dúvida, valendo-se de um experimento de calorimetria baseado no fato de que metais diferentes possuem diferentes calores específicos.
Inicialmente, a estudante deixou o anel de 4,0 g por um longo tempo dentro de uma vasilha com água fervente (100 ºC). Tirou, então, o anel dessa vasilha e o mergulhou em um outro recipiente, bem isolado termicamente, contendo 2 ml de água a 15 ºC. Mediu a temperatura final da água em equilíbrio térmico com o anel. O calor específico da água é igual a 1,0 cal/gºC, e sua densidade é igual a 1,0 g/cm3. Despreze a troca de calor entre a água e o recipiente.
a) Sabendo-se que o calor específico do ouro é cAu = 0,03 cal/g0C, qual deveria ser a temperatura final de equilíbrio se o anel fosse de ouro puro?
b) A temperatura final de equilíbrio medida pela estudante foi de 22 ºC. Encontre o calor específico do anel.
c) A partir do gráfico e da tabela abaixo, determine qual é a porcentagem de ouro do anel e quantos quilates ele tem.
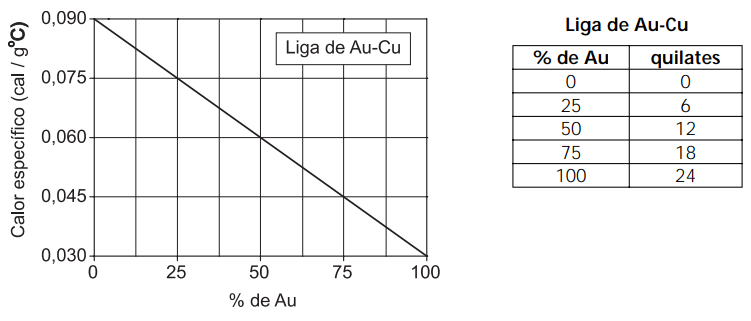
.
Ver questãoQuestão 51643
UNICAMP
(UNICAMP - 2006 - 2 FASE ) As baleias são mamíferos aquáticos dotados de um sistema respiratório altamente eficiente que dispensa um acúmulo muito elevado de ar nos pulmões, o que prejudicaria sua capacidade de submergir. A massa de certa baleia é de 1,50 × 105 kg e o seu volume, quando os pulmões estão vazios, é igual a 1,35 × 102 m3.
a) Calcule o volume máximo da baleia após encher os pulmões de ar, acima do qual a baleia não conseguiria submergir sem esforço. Despreze o peso do ar nos pulmões e considere a densidade da água do mar igual a 1,0 × 103 kg/m3.
b) Qual é a variação percentual do volume da baleia ao encher os pulmões de ar até atingir o volume máximo calculado no item a? Considere que inicialmente os pulmões estavam vazios.
c) Suponha que uma baleia encha rapidamente seus pulmões em um local onde o ar se encontra inicialmente a uma temperatura de 7 ºC e a uma pressão de 1,0 atm (1,0 × 105 N/m2). Calcule a pressão do ar no interior dos pulmões da baleia, após atingir o equilíbrio térmico com o corpo do animal, que está a 37 0C. Despreze qualquer variação da temperatura do ar no seu caminho até os pulmões e considere o ar um gás ideal.
Questão 51644
UNICAMP
(UNICAMP - 2006 - 2 FASE ) Pares metálicos constituem a base de funcionamento de certos disjuntores elétricos, que são dispositivos usados na proteção de instalações elétricas contra curtos-circuitos. Considere um par metálico formado por uma haste de latão e outra de aço, que, na temperatura ambiente, têm comprimento L = 4,0 cm. A variação do comprimento da haste, L, devida a uma variação de temperatura , é dada por
, onde
é o coeficiente de dilatação térmica linear do material.
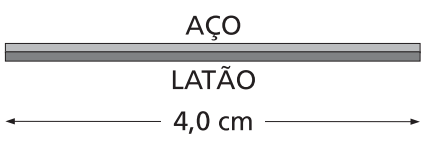
a) Se a temperatura aumentar de 60 ºC, qual será a diferença entre os novos comprimentos das hastes de aço e de latão? Considere que as hastes não estão presas uma à outra, e que Lat =1,9 × 10-5 ºC-1 e Aço = 1,3 × 10-5 ºC-1.
b) Se o aquecimento se dá pela passagem de uma corrente elétrica de 10 A e o par tem resistência de 2,4 x 10-3 , qual é a potência dissipada?
Questão 51645
UNICAMP
(UNICAMP - 2006 - 2 FASE ) O gráfico abaixo mostra a resistividade elétrica de um fi o de nióbio (Nb) em função da temperatura. No gráfico, pode-se observar que a resistividade apresenta uma queda brusca em T = 9,0 K, tornando-se nula abaixo dessa temperatura. Esse comportamento é característico de um material supercondutor.
Um fio de Nb de comprimento total L = 1,5 m e seção transversal de área A = 0,050 mm2 é esticado verticalmente do topo até o fundo de um tanque de hélio líquido, a fim de ser usado como medidor de nível, conforme ilustrado na fi gura abaixo. Sabendo-se que o hélio líquido se encontra a 4,2 K e que a temperatura da parte não imersa do fio fica em torno de 10 K, pode-se determinar a altura h do nível de hélio líquido através da medida da resistência do fio.
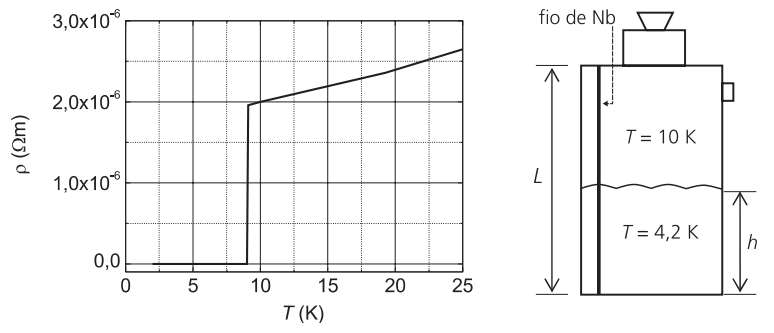
a) Calcule a resistência do fio quando toda a sua extensão está a 10 K, isto é, quando o tanque está vazio.
b) Qual é a altura h do nível de hélio líquido no interior do tanque em uma situação em que a resistência do fi o de Nb vale 36 ?
Questão 51646
UNICAMP
(UNICAMP - 2006 - 2 FASE ) A utilização de campos elétrico e magnético cruzados é importante para viabilizar o uso da técnica híbrida de tomografia de ressonância magnética e de raios X.
A figura abaixo mostra parte de um tubo de raios X, onde um elétron, movendo-se com velocidade v = 5,0 × 105 m/s ao longo da direção x, penetra na região entre as placas onde há um campo magnético uniforme, , dirigido perpendicularmente para dentro do plano do papel. A massa do elétron é me = 9 × 10-31 kg e a sua carga elétrica é q = -1,6 × 10-19 C. O módulo da força magnética que age sobre o elétron é dado por
, onde
é o ângulo entre a velocidade e o campo magnético.
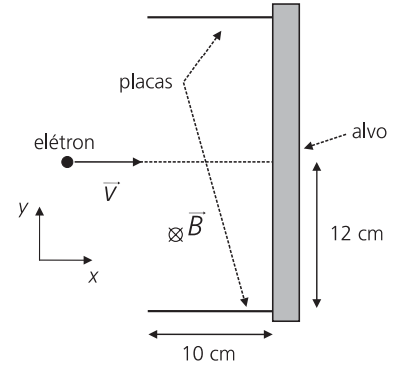
a) Sendo o módulo do campo magnético B = 0,010 T, qual é o módulo do campo elétrico que deve ser aplicado na região entre as placas para que o elétron se mantenha em movimento retilíneo uniforme?
b) Numa outra situação, na ausência de campo elétrico, qual é o máximo valor de B para que o elétron ainda atinja o alvo? O comprimento das placas é de 10 cm.