GuruGuia

Questão 76428

CEFET-MG

(CFTMG 2020) Considere as funções reais $f(x)=-2x^2+6x e g(x)=x^2+1$ .

A quantidade de números inteiros que satisfazem a inequação $frac{f(x)}{g(x)}>0$ é igual

Gabarito:

Resolução:

Considere as funções reais $f(x)=-2x^2+6x e g(x)=x^2+1$ .

A quantidade de números inteiros que satisfazem a inequação é igual

$frac{f(x)}{g(x)}>0$

$frac{-2x^2+6x}{x^2+1} > 0$

♦ $-2x^2+6x=0$

$-2x(x-3)=0$ → 0 e 3 são raízes.

♦ $x^2+1=0$ → não tem raízes reais.

Estudo de sinais:

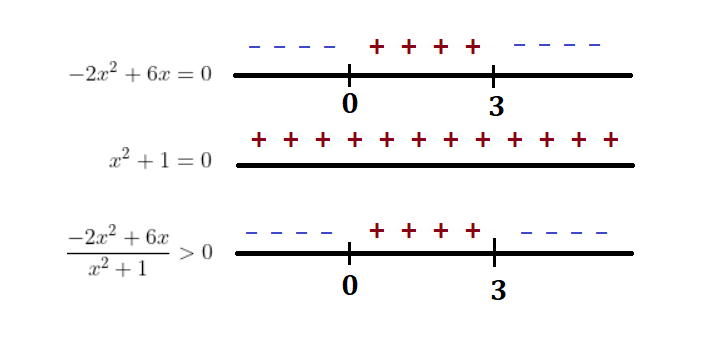
Intervalo solução: $0 < x< 3$

Números inteiros nesse intervalo: 1 e 2.

Alternativa correta é Letra B.

Questão 2616

CEFET-MG

(CEFET - MG - 2006)

A regência nominal está conforme a norma culta em:

Ver questão

Questão 5874

CEFET-MG

(CEFET - 2011) Numa pesquisa com 2000 pessoas no Bairro Nova Cintra sobre a audiência de três programas de TV, obteve-se o seguinte resultado:

Programas	Nº de telespectadores
A	1220
B	400
C	1080
A e B	220
A e C	800
B e C	180
A, B e C	100

Analisando os resultados, a porcentagem de telespectadores que não assistem a nenhum desses programas é

Ver questão

Questão 5875

CEFET-MG

(CEFET - 2010) A é o conjunto dos divisores de 30 e B o conjunto dos números constituídos pela soma de dois elementos distintos de A. Desse modo, o conjunto que NÃO possui interseção com B é

Ver questão

Questão 5876

CEFET-MG

(CEFET - 2010) Uma enquete intitulada "O que mais falta no seu celular?" foi realizada em um site da internet, apresentando o seguinte resultado:

Itens do celular	Nº de Internautas
TV	97
Touch Screen	44
Wi Fi	37
TV e Touch Screen	10
Wi Fi e Touch Screen	15
Wi Fi e TV	18
Wi Fi e TV e Touch Screen	5
Nenhum	15

O número de internautas que responderam a essa enquete foi

Ver questão