FUVEST 2013
Questão 36324
FUVEST
| (Fuvest 2013 2 fase) |
Um DJ, ao preparar seu equipamento, esquece uma caixa de fósforos sobre o disco de vinil, em um toca-discos desligado. A caixa se encontra a 10 cm do centro do disco. Quando o toca-discos é ligado, no instante t = 0, ele passa a girar com aceleração angular constante α = 1,1 rad/s2, até que o disco atinja a frequência final f = 33 rpm que permanece constante. O coeficiente de atrito estático entre a caixa de fósforos e o disco é = 0,09. Determine
a) a velocidade angular final do disco, , em rad/s;
b) o instante tf em que o disco atinge a velocidade angular ;
c) a velocidade angular do disco no instante tc em que a caixa de fósforos passa a se deslocar em relação ao mesmo;
d) o ângulo total percorrido pela caixa de fósforos desde o instante t = 0 até o instante t = tc.
Note e adote: Aceleração da gravidade local g =10 m/s2 e π = 3
Ver questãoQuestão 36325
FUVEST
| (Fuvest 2013 2 fase) |
Em uma aula de laboratório, os alunos determinaram a força eletromotriz ε e a resistência interna r de uma bateria. Para realizar a tarefa, montaram o circuito representado na figura abaixo e, utilizando o voltímetro, mediram a diferença de potencial V para diferentes valores da resistência R do reostato. A partir dos resultados obtidos, calcularam a corrente I no reostato e construíram a tabela apresentada na página de respostas.
a) Complete a tabela, na página de respostas, com os valores da corrente I.
b) Utilizando os eixos da página de respostas, faça o gráfico de V em função de I.
c) Determine a força eletromotriz ε e a resistência interna r da bateria.
Note e adote:
Um reostato é um resistor de resistência variável.
Ignore efeitos resistivos dos fios de ligação do circuito.
Questão 36327
FUVEST
| (Fuvest 2013 2 fase) |
A potência elétrica instalada no Brasil é 100 GW. Considerando que o equivalente energético do petróleo seja igual a 4x107 J/L, que a potência média de radiação solar por unidade de área incidente na superfície terrestre seja igual a 250 W/m2 e que a relação de equivalência entre massa m e energia E é expressa por E = mc2, determine
a) a área A de superfície terrestre, na qual incide uma potência média de radiação solar equivalente à potência elétrica instalada no Brasil;
b) a energia elétrica EB consumida no Brasil em um ano, supondo que, em média, 80% da potência instalada seja utilizada;
c) o volume V de petróleo equivalente à energia elétrica consumida no Brasil em um ano;
d) a massa m equivalente à energia elétrica consumida no Brasil em um ano.
Note e adote:
1 GW = 109 W
c = 3 x 108 m/s
1 ano = 3 x 107 s
Questão 36385
UNICAMP
(UNICAMP - 2013 - 2 fase - Questão 13)
Em 14 de outubro de 2012, Felix Baumgartner quebrou o recorde de velocidade em queda livre. O salto foi monitorado oficialmente e os valores obtidos estão expressos de modo aproximado na tabela e no gráfico abaixo.
a) Supondo que a velocidade continuasse variando de acordo com os dados da tabela, encontre o valor da velocidade, em km/h, no 30º segundo.
b) Com base no gráfico, determine o valor aproximado da velocidade máxima atingida e o tempo, em segundos, em que Felix superou a velocidade do som. Considere a velocidade do som igual a 1.100 km/h.
Questão 36386
UNICAMP
(UNICAMP - 2013 - 2 fase - Questão 14)
Os lados do triângulo ABC da figura abaixo têm as seguintes medidas: e
a) Sobre o lado BC marca-se um ponto D tal que e traça-se o segmento DE paralelo ao lado AC, Ache a razão entre a altura H do triângulo ABC relativa ao lado AC e a altura h do triângulo EBD relativa ao lado ED, sem explicitar os valores de h e H.
b) Calcule o valor explícito da altura do triângulo ABC em relação ao lado AC
Ver questãoQuestão 36387
UNICAMP
(UNICAMP - 2013 - 2 fase - Questão 15)
A superfície de um reservatório de água para abastecimento público tem 320.000 m2 de área, formato retangular e um dos seus lados mede o dobro do outro. Essa superfície é representada pela região hachurada na ilustração abaixo. De acordo com o Código Florestal, é necessário manter ao redor do reservatório uma faixa de terra livre, denominada Área de Proteção Permanente (APP), como ilustra a figura abaixo.Essa faixa deve ter largura constante e igual a 100m, medidos a partir da borda do reservatório.
a) Calcule a área da faixa de terra denominada APP nesse caso.
b) Suponha que a água do reservatório diminui de acordo com a expressão em que V0 é o volume inicial e t é o tempo decorrido em meses. Qual é o tempo necessário para que o volume se reduza a 10% do volume inicial? Utilize, se ncessário,
Ver questão
Questão 36388
UNICAMP
(UNICAMP - 2013 - 2 fase - Questão 16)
A numeração dos calçados obedece a padrões distintos, conforme o país. No Brasil, essa numeração varia de um em um, e vai de 33 a 45, para adultos. Nos Estados Unidos a numeração varia de meio em meio, e vai de 3,5 a 14 para homens e de 5 a 15,5 para mulheres.
a) Considere a tabela abaixo.
Suponha que as grandezas estão relacionadas por funções afins t(x) = ax +b para a numeração brasileira e x(t) = ct + d para o comprimento do calçado. Encontre os valores dos parâmetros a e b da expressão que permite obter a numeração dos calçados brasileiros em termos do comprimento, ou os valores dos parâmetros c e d da expressão que fornece o comprimento em termos da numeração.
b) A numeração dos calçados femininos nos Estados Unidos pode ser estabelecida de maneira aproximada pela função real f definida por f(x) = 5(x - 20)/3 , em que x é o comprimento do calçado em cm. Sabendo que a numeração dos calçados nk forma uma progressão aritmética de razão 0,5 e primeiro termo n1 = 5 , em que nk = f(ck) , com k natural, calcule o comprimento c5 .
Ver questãoQuestão 36389
UNICAMP
(UNICAMP - 2013 - 2 fase - Questão 17)
Na formulação de fertilizantes, os teores percentuais dos macronutrientes N, P e K, associados respectivamente a nitrogênio, fósforo e potássio, são representados por x , y e z .
a) Os teores de certo fertilizante satisfazem o seguinte sistema de equações lineares:
Calcule x e y nesse caso.
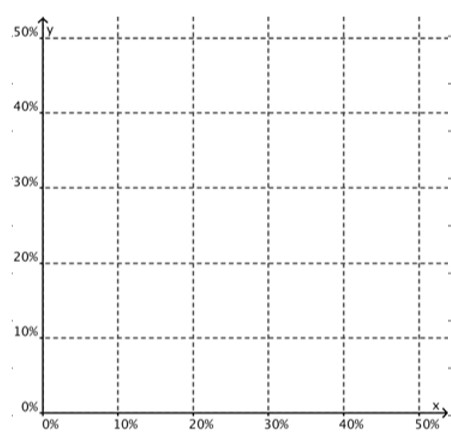
b) Suponha que para outro fertilizante valem as relações 24% ≤ x + y + z ≤ 54% , x ≥ 10% , y ≥ 20% e z = 10%. Indique no plano cartesiano abaixo a região de teores (x, y) admissíveis para tal fertilizante.
Questão 36390
UNICAMP
(UNICAMP - 2013 - 2 fase - Questão 18)
O diagrama abaixo indica a distribuição dos alunos matriculados em três cursos de uma escola. O valor da mensalidade de cada curso é de R$ 600,00, mas a escola oferece descontos aos alunos que fazem mais de um curso. Os descontos, aplicados sobre o valor total da mensalidade, são de 20% para quem faz mais dois cursos e de 30% para os matriculados em três cursos.
a) Por estratégia de marketing, suponha que a escola decida divulgar os percentuais de desconto, calculados sobre a mensalidade dos cursos adicionais e não sobre o total da mensalidade. Calcule o percentual de desconto que incide sobre a mensalidade do segundo curso para aqueles que fazem dois cursos e o percentual de desconto sobre o terceiro curso para aqueles que fazem três cursos.
b) Com base nas informações do diagrama, encontre o número dos alunos matriculados em pelo menos dois cursos. Qual a probabilidade de um aluno, escolhido ao acaso, estar matriculado em apenas um curso?
Questão 36391
UNICAMP
(UNICAMP - 2013 - 2 fase - Questão 19)
Considere a família de retas no plano cartesiano descrita pela equação (2 - p)x + (2p + 1)y + 8p + 4 = 0, nas variáveis x e y , em que p é um parâmetro real.
a) Determine o valor do parâmetro p para que a reta correspondente intercepte perpendicularmente o eixo y . Encontre o ponto de interseção neste caso.
b) Considere a reta x + 3y + 12 = 0 dessa família para p = 1. Denote por A o seu ponto de interseção com o eixo x e por O a origem do plano cartesiano. Exiba a equação da circunferência em que o segmento OA é um diâmetro.
Ver questão