Dados e ݊ inteiros, considere a função ݂ definida por
para
a) No caso em que , mostre que a igualdade se verifica.
b) No caso em que , ache as interseções do gráfico de com os eixos coordenados.
c) No caso em que , esboce a parte do gráfico de em que , levando em conta as informações obtidas nos itens a) e b). Utilize o par de eixos dado na página de de respostas (imagem abaixo).
d) Existe um par de inteiros tal que a condição continue sendo satisfeita?
Gabarito:
Resolução:
Sendo, com x diferente de -n e m=n e igual à, então:
a)
b) Sendo A(x,0) a intersecção de f com o eixo x, logo:
Caso a intersecção com o eixo y, teremos:
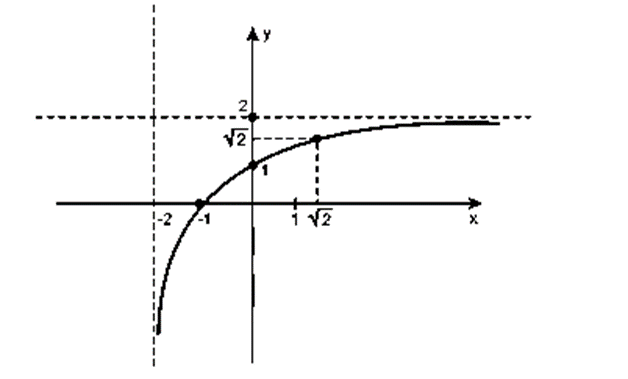
c) O gráfico de f, contém os pontos e .
Quando x tender a-2, sempre com valores maiores que -2, f(x) tende a - infinito.
Caso c tender a + infinito, tende a zero e f(x) tende a 2. Logo teremos a seguinte representação gráfica:
Omolu espalhara a bexiga na cidade. Era uma vingança contra a cidade dos ricos. Mas os ricos tinham a vacina, que sabia Omolu de vacinas? Era um pobre deus das florestas d’África. Um deus dos negros pobres. Que podia saber de vacinas? Então a bexiga desceu e assolou o povo de Omolu. Tudo que Omolu pôde fazer foi transformar a bexiga de negra em alastrim, bexiga branca e tola. Assim mesmo morrera negro, morrera pobre. Mas Omolu dizia que não fora o alastrim que matara. Fora o 1lazareto. Omolu só queria com o alastrim marcar seus filhinhos negros. O lazareto é que os matava. Mas as macumbas pediam que ele levasse a bexiga da cidade, levasse para os ricos latifundiários do sertão. Eles tinham dinheiro, léguas e léguas de terra, mas não sabiam tampouco da vacina. O Omolu diz que vai pro sertão. E os negros, os ogãs, as filhas e pais de santo cantam:
Ele é mesmo nosso pai e é quem pode nos ajudar...
Omolu promete ir. Mas para que seus filhos negros não o esqueçam avisa no seu cântico de despedida:
Ora, adeus, ó meus filhinhos, Qu’eu vou e torno a vortá...
E numa noite que os atabaques batiam nas macumbas, numa noite de mistério da Bahia, Omolu pulou na máquina da Leste Brasileira e foi para o sertão de Juazeiro. A bexiga foi com ele.
Jorge Amado, Capitães da Areia.
1lazareto: estabelecimento para isolamento sanitário de pessoas atingidas por determinadas doenças.
Costuma-se reconhecer que Capitães da Areia pertence ao assim chamado “romance de 1930”, que registra importantes transformações pelas quais passava o Modernismo no Brasil, à medida que esse movimento se expandia e diversificava. No excerto, considerado no contexto do livro de que faz parte, constitui marca desse pertencimento
Como não expressa visão populista nem elitista, o livro não idealiza os pobres e rústicos, isto é, não oculta o dano causado pela privação, nem os representa como seres desprovidos de vida interior; ao contrário, o livro trata de realçar, na mente dos desvalidos, o enlace estreito e dramático de limitação intelectual e esforço reflexivo.
Essas afirmações aplicam-se ao modo como, na obra:
