Questão 36368
FUVEST
(FUVEST - 2018 - 2a fase)
Sejam C um subconjunto não vazio e P um ponto, ambos em um mesmo plano, tais que P C. Diz-se que “P enxerga C sob um ângulo
" se
for a medida do menor ângulo com vértice em P que contenha C. Por exemplo, na figura, o ponto P enxerga o quadrado C sob o ângulo
indicado.
a) Se for um círculo de raio r, centrado na origem de um plano cartesiano real, determine o lugar geométrico dos pontos que enxergam C sob um ângulo de 60° .
b) Se for a união dos segmentos OA e OB , em que A = (a, 0) e B = (0,b), com a,b > 0, determine o lugar geométrico dos pontos que enxergam C sob um ângulo de 90°.
Gabarito:
Resolução:
Em construção:
a)
Pelo desenho, podemos observar que:
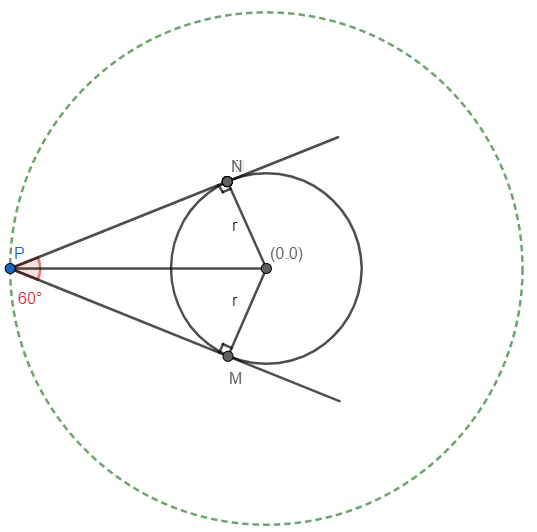
Devido à simetria, o segmento OP é bissetriz do ângulo em P e pela propriedade de tangência, PN e PM formam ângulos retos com os raios da circunferência.
Logo, temos dois triângulos retângulos PNO e PMO e seus ângulos em P valem 30° cada um. Sendo assim, podemos usar a trigonometria:
logo:
Notamos que, por simetria, qualquer ponto da circunferência verde tracejada enxergará o círculo sobre essas mesmas condições. Portanto, o lugar geométrico dos pontos será a circunferência de raio 2r centrada na origem. Sua equação é:
_______________________________________________________________________________________________
b)
Os pontos que enxergam um segmento de reta sob o ângulo de 90° formam uma semi-circunferência. Dessa maneira, obtemos:
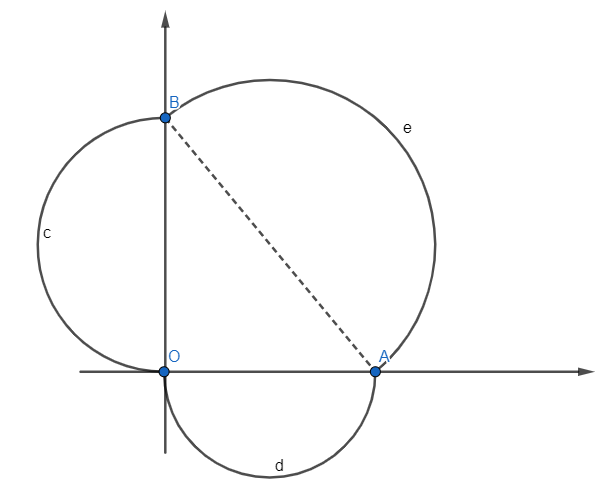
Vemos que o semicírculo c "enxerga" o segmento OB, o semicírculo d enxerga o segmento OA e o semicírculo e enxerga o segmento AB. Sendo assim, basta determinar as equações desses semicírculos:
semicírculo c (para x<0)
Centro:
Raio:
Equação:
-----------------------------------------------
semicírculo d (para y<0)
Centro:
Raio:
Equação:
------------------------------------------------
semicírculo e (para x e y >0)
Centro:
Raio:
Equação: