GuruGuia

Questão 44348

FUVEST

(FUVEST - 2012)

A base do tetraedro PABCD é o quadrado ABCD de lado L, contido no plano α. Sabe-se que a projeção ortogonal do vértice P no plano α está no semiplano de α determinado pela reta BC e que não contém o lado AD. Além disso, a face DPC é um triângulo isósceles de base BC Cuja altura forma, com o plano α, um ângulo θ, em que 0 < θ < π/2. Sendo PB = $L frac {sqrt 2}2$ , determine, em função de L e θ,

a) o volume do tetraedro PABCD;

b) a altura do triângulo APB relativa ao lado AB;

c) a altura do triângulo APD relativa ao lado AD.

Gabarito:

Resolução:

RESOLVENDO A LETRA (A):

Sabemos que o volume $V$ de uma pirâmide é:

$V= frac{A_bcdot h}{3}$

Já temos a área da base e precisamos apenas da altura. Para encontrar a altura temos que perceber que:

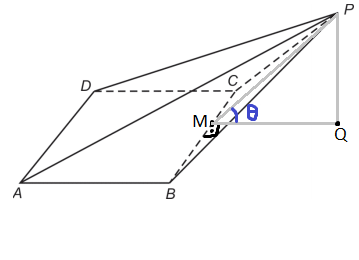
Onde $M$ é ponto médio de $BC$ .

A altura é $overline{PQ}$ e percebemos que $sin{( heta)} = frac{PQ}{MP}$ então devemos encontrar $MP$ para podermos escrever $PQ$ em função de $heta$ e $l$ .

Fazendo pitágoras em $MPB$ :

$(frac{lsqrt{2}}{2})^2 = (frac{l}{2})^2 + MP^2$

$frac{2l^2}{4} = frac{l^2}{4} + MP^2$

$MP = frac{l}{2}$

Agora podemos encontrar $PQ$ em função de $heta$ e $l$ da seguinte forma:

$sin{( heta)} = frac{PQ}{frac{l}{2}}$

$sin{( heta)} cdot frac{l}{2}= PQ$

Substituindo na fórmula do volume:

$V= frac{A_bcdot h}{3}$

$V= frac{l^2}{3} cdot frac{sin{ heta}cdot l}{2}$

$V= frac{l^3 cdot sin{ heta}}{6}$

RESOLVENDO A LETRA (B):

Fazendo o desenho das informações a questão nos dá:

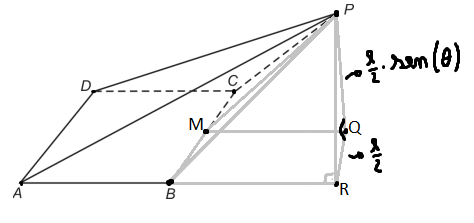
Podemos perceber então que basta aplicar o teorema de Pitágoras no triângulo PQR:

$PR^2 = (frac{l}{2})^2 + (frac{l cdot sin{( heta)}}{2})^2$

$PR^2 = frac{l^2}{4} + frac{l^2 cdot sin^2{( heta)}}{4}$

$PR^2 = frac{l^2}{4}(1 + sin^2{( heta)})$

$PR = frac{l}{2}sqrt{1 + sin^2{( heta)}}$

RESOLVENDO A LETRA (C):

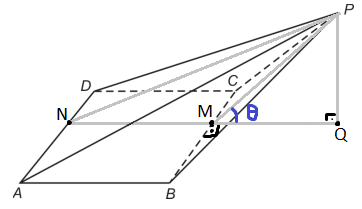
Podemos perceber que como já temos $overline{PQ}$ e $overline{NM}$ , podemos encontrar $overline{NP}$ por teorema de Pitágoras em $NPQ$ , basta encontrarmos $overline{MQ}$ .

Fazendo:

$cos{ heta} = frac{MQ}{MP}$

$cos{ heta} = frac{MQ}{frac{l}{2}}$

$frac{l}{2}cdot cos{ heta} = MQ$

Fazendo Pítagoras em NPQ:

$PN^2 = (frac{l cdot sin{ heta}}{2})^2 + (l+frac{lcdot cos{ heta}}{2})^2$

$PN^2 = frac{l^2 cdot sin^2{ heta}}{4} + l^2+2cdot l cdot frac{lcdot cos{ heta}}{2} + frac{l^2cdot cos^2{ heta}}{4}$

$PN^2 = frac{5}{4}l^2 + l^2cos{ heta}$

$PN^2 = l^2(frac{5}{4} + cos{ heta})$

$PN = frac{lsqrt{5 + 4cos{ heta}}}{2}$

Questão 1779

FUVEST

(FUVEST - 2016 - 1ª FASE)

No contexto do cartum, a presença de numerosos animais de estimação permite que o juízo emitido pela personagem seja considerado

Ver questão

Questão 1780

FUVEST

(FUVEST - 2016 - 1ª FASE)

Para obter o efeito de humor presente no cartum, o autor se vale, entre outros, do seguinte recurso:

Ver questão

Questão 1794

FUVEST

(Fuvest 2016)

Omolu espalhara a bexiga na cidade. Era uma vingança contra a cidade dos ricos. Mas os ricos tinham a vacina, que sabia Omolu de vacinas? Era um pobre deus das florestas d’África. Um deus dos negros pobres. Que podia saber de vacinas? Então a bexiga desceu e assolou o povo de Omolu. Tudo que Omolu pôde fazer foi transformar a bexiga de negra em alastrim, bexiga branca e tola. Assim mesmo morrera negro, morrera pobre. Mas Omolu dizia que não fora o alastrim que matara. Fora o¹lazareto. Omolu só queria com o alastrim marcar seus filhinhos negros. O lazareto é que os matava. Mas as macumbas pediam que ele levasse a bexiga da cidade, levasse para os ricos latifundiários do sertão. Eles tinham dinheiro, léguas e léguas de terra, mas não sabiam tampouco da vacina. O Omolu diz que vai pro sertão. E os negros, os ogãs, as filhas e pais de santo cantam:

Ele é mesmo nosso pai
e é quem pode nos ajudar...

Omolu promete ir. Mas para que seus filhos negros não o esqueçam avisa no seu cântico de despedida:

Ora, adeus, ó meus filhinhos,
Qu’eu vou e torno a vortá...

E numa noite que os atabaques batiam nas macumbas, numa noite de mistério da Bahia, Omolu pulou na máquina da Leste Brasileira e foi para o sertão de Juazeiro. A bexiga foi com ele.

Jorge Amado, Capitães da Areia.

¹lazareto: estabelecimento para isolamento sanitário de pessoas atingidas por determinadas doenças.

Costuma-se reconhecer que Capitães da Areia pertence ao assim chamado “romance de 1930”, que registra importantes transformações pelas quais passava o Modernismo no Brasil, à medida que esse movimento se expandia e diversificava. No excerto, considerado no contexto do livro de que faz parte, constitui marca desse pertencimento

Ver questão

Questão 1804

FUVEST

(Fuvest 2012)

Como não expressa visão populista nem elitista, o livro não idealiza os pobres e rústicos, isto é, não oculta o dano causado pela privação, nem os representa como seres desprovidos de vida interior; ao contrário, o livro trata de realçar, na mente dos desvalidos, o enlace estreito e dramático de limitação intelectual e esforço reflexivo.

Essas afirmações aplicam-se ao modo como, na obra:

Ver questão