Questão 45041
FUVEST
(FUVEST - 2009 - 2 fase - Questão 10)
A figura representa uma pirâmide ABCDE, cuja base é o retângulo ABCD. Sabe-se que
Nessas condições, determine:
a) A medida de BP .
b) A área do trapézio BCQP .
c) O volume da pirâmide BPQCE .
Gabarito:
Resolução:
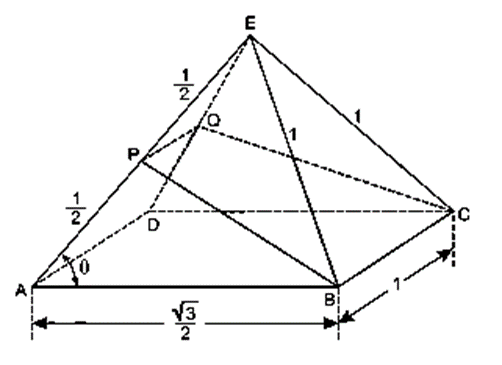
a) Sendo a medida do ângulo agudo
, no triângulo
, temos que:
e no triângulo teremos:
Logo,
b) Sendo h a altura do trapézio isósceles e
a sua área teremos:
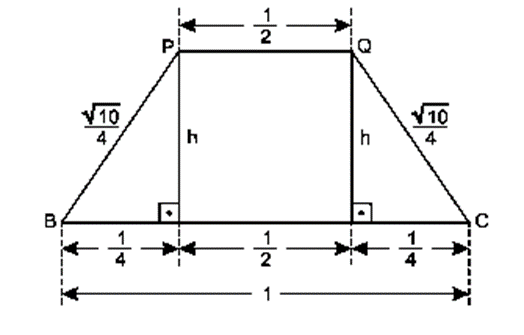
, pois h deverá ser maior que 0.
Dessa forma,
c)
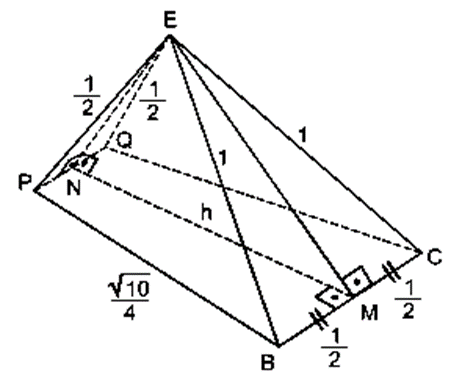
Sendo e
os pontos médios dos segmentos
e
, teremos:
e
Logo podemos concluir que o triângulo é retângulo em
, pois
uma vez que
, portanto,
é a altura da pirâmide
, pois
é perpendicular ao
Portanto, o volume dessa pirâmide será: