GuruGuia

Questão 60248

FUVEST

(FUVEST - 2021 - 2ª FASE)

O perímetro de uma figura plana é o comprimento de seu contorno. O diâmetro de uma figura plana é a maior distância entre dois pontos do contorno dessa figura. Calcule a razão entre o perímetro e o diâmetro em cada uma das figuras planas nos casos a seguir:

a) Um retângulo com lados de medidas 3 e 4.

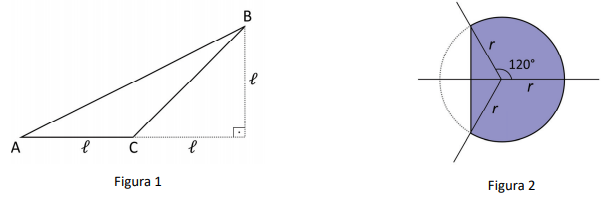
b) O triângulo obtusângulo ABC mostrado na Figura 1.

c) A região colorida dentro do círculo de raio 𝑟 mostrada na Figura 2.

Gabarito:

Resolução:

a) O retângulo seria como desenhado abaixo:

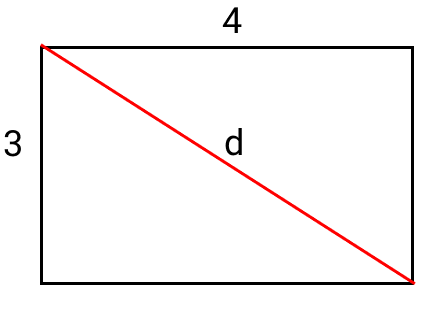
Como o diâmetro é a maior distância entre dois pontos localizados sobre o perímetro da figura, então o diâmetro do retângulo deve ser sua diagonal. Assim:

Diâmetro: $d=sqrt{3^2+4^2}=sqrt{9+16}=sqrt{25}=5$

Perímetro: $2p=2cdotleft(3+4 ight )=2cdot7=14$

RAZÃO: $frac{2p}{d}=frac{14}{5}$

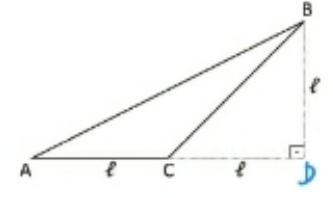
Primeiramente obtemos, por Pitágoras, o valor do lado CB do triângulo retângulo CDB:

$CB=sqrt{CD^2+DB^2}=sqrt{l^2+l^2}=lsqrt{2}$

Para descobrirmos AB podemos fazer Pitágoras em ADB:

$AB=sqrt{AD^2+DB^2}=sqrt{left(2l ight )^2+l^2}=lsqrt{5}$

Com o valor dos lados desse triângulo ABC em mãos podemos calcular o perímetro e diâmetro do mesmo.

Como o diâmetro é a maior distância entre pontos do perímetro do triângulo, a maior distância obtida entre dois pontos de um triângulo é o próprio lado maior desse triângulo. No caso desse triângulo, o maior lado é AB, logo:

Diâmetro: $d=AB=lsqrt{5}$

Perímetro: $2p=AC+CB+BA=l+lsqrt{2}+lsqrt{5}Rightarrow 2p=lleft(1+sqrt{2}+sqrt{5} ight )$

RAZÃO: $frac{2p}{d}=frac{lleft(1+sqrt{2}+sqrt{5} ight )}{lsqrt{5}}=frac{1+sqrt{2}+sqrt{5}}{sqrt{5}}cdotleft(frac{sqrt{5}}{sqrt{5}} ight )Rightarrow frac{2p}{d}=frac{sqrt{5}+sqrt{10}+5}{5}=1+sqrt{5}cdotleft(frac{1+sqrt{2}}{5} ight )$

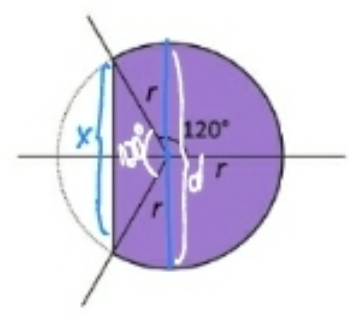
Perceba que os três ângulos centrais dessa figura circular são todos iguais a 120°.

No triângulo destacado de lados r, r e x podemos fazer Lei dos Cossenos para obtermos x em função a r:

$x^2=r^2+r^2-2cdot rcdot rcdotleft(cosleft(120^{circ} ight ) ight )=2r^2-2r^2cdotleft(frac{-1}{2} ight )=2r^2left(1+frac{1}{2} ight )Rightarrow$

$Rightarrow x^2=3r^2Rightarrow x=rsqrt{3}$

O diâmetro dessa figura é o próprio diâmetro do círculo que é 2r.

Já o perímetro é igual a x mais o perímetro do setor circular direito. Veja que dividindo o círculo em três partes iguais, ou seja, em três setores de 120° cada (já que o círculo tem 360° como ângulo central, então 360° / 3 = 120° para cada setor). Então, cada setor circular de 120° possui perímetro igual a um terço do perímetro de um círculo normal. Como esta figura na parte direita é a junção de dois setores circulares de 120° cada, então o perímetro dessa parte é dois terços do perímetro do círculo completo. Assim:

Diâmetro: $d=2r$

Perímetro: $2p=x+2cdotleft(perimetro,setor,circular,120^{circ} ight )=x+2cdotleft(frac{2pi r}{3} ight )=rsqrt{3}+rcdotfrac{4pi}{3}$

RAZÃO: $frac{2p}{d}=frac{rsqrt{3}+rcdotfrac{4pi}{3}}{2r}=frac{3sqrt{3}+4pi}{6}$

Questão 1779

FUVEST

(FUVEST - 2016 - 1ª FASE)

No contexto do cartum, a presença de numerosos animais de estimação permite que o juízo emitido pela personagem seja considerado

Ver questão

Questão 1780

FUVEST

(FUVEST - 2016 - 1ª FASE)

Para obter o efeito de humor presente no cartum, o autor se vale, entre outros, do seguinte recurso:

Ver questão

Questão 1794

FUVEST

(Fuvest 2016)

Omolu espalhara a bexiga na cidade. Era uma vingança contra a cidade dos ricos. Mas os ricos tinham a vacina, que sabia Omolu de vacinas? Era um pobre deus das florestas d’África. Um deus dos negros pobres. Que podia saber de vacinas? Então a bexiga desceu e assolou o povo de Omolu. Tudo que Omolu pôde fazer foi transformar a bexiga de negra em alastrim, bexiga branca e tola. Assim mesmo morrera negro, morrera pobre. Mas Omolu dizia que não fora o alastrim que matara. Fora o¹lazareto. Omolu só queria com o alastrim marcar seus filhinhos negros. O lazareto é que os matava. Mas as macumbas pediam que ele levasse a bexiga da cidade, levasse para os ricos latifundiários do sertão. Eles tinham dinheiro, léguas e léguas de terra, mas não sabiam tampouco da vacina. O Omolu diz que vai pro sertão. E os negros, os ogãs, as filhas e pais de santo cantam:

Ele é mesmo nosso pai
e é quem pode nos ajudar...

Omolu promete ir. Mas para que seus filhos negros não o esqueçam avisa no seu cântico de despedida:

Ora, adeus, ó meus filhinhos,
Qu’eu vou e torno a vortá...

E numa noite que os atabaques batiam nas macumbas, numa noite de mistério da Bahia, Omolu pulou na máquina da Leste Brasileira e foi para o sertão de Juazeiro. A bexiga foi com ele.

Jorge Amado, Capitães da Areia.

¹lazareto: estabelecimento para isolamento sanitário de pessoas atingidas por determinadas doenças.

Costuma-se reconhecer que Capitães da Areia pertence ao assim chamado “romance de 1930”, que registra importantes transformações pelas quais passava o Modernismo no Brasil, à medida que esse movimento se expandia e diversificava. No excerto, considerado no contexto do livro de que faz parte, constitui marca desse pertencimento

Ver questão

Questão 1804

FUVEST

(Fuvest 2012)

Como não expressa visão populista nem elitista, o livro não idealiza os pobres e rústicos, isto é, não oculta o dano causado pela privação, nem os representa como seres desprovidos de vida interior; ao contrário, o livro trata de realçar, na mente dos desvalidos, o enlace estreito e dramático de limitação intelectual e esforço reflexivo.

Essas afirmações aplicam-se ao modo como, na obra:

Ver questão