Questão 60250
FUVEST
(FUVEST - 2021 - 2ª FASE)
Considere a função 𝑓: ℝ → ℝ dada por 𝑓(𝑥) = 𝑝 + 𝑞 cos(𝑟𝑥 − 𝑠), em que 𝑝, 𝑞, 𝑟 e 𝑠 são números reais e o cosseno é calculado sobre valores em radianos.
a) Qual é o valor máximo de 𝑓 para o caso em que 𝑝 = 𝑞 = 𝑟 = 𝑠 = 1?
b) Quais são os valores do período e da amplitude de 𝑓, para o caso em que 𝑝 = −1, 𝑞 = 2, 𝑟 = 𝜋 e 𝑠 = 0?
c) Determine valores de 𝑝, 𝑞, 𝑟 e 𝑠 no caso em que o gráfico de 𝑓 é igual ao mostrado na figura a seguir.
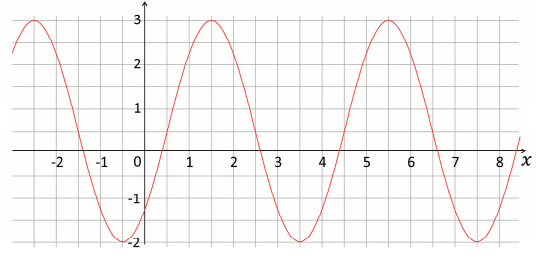
Note e adote: A amplitude de uma função é a diferença entre seus valores máximo e mínimo. O gráfico apresentado refere-se somente ao item (c).
Gabarito:
Resolução:
a) Se 𝑝 = 𝑞 = 𝑟 = 𝑠 = 1, então 𝑓(𝑥) = 𝑝 + 𝑞 cos(𝑟𝑥 − 𝑠) => f(x) = 1 + cos(x - 1).
O valor máximo de f seria para quando cos(x-1) fosse máximo e isto acontece para valores de x tais que x - 1 = 2π, pois assim cos(x-1) = cos(2π) = 1.
Daí, f máximo seria igual a f(xmáx.) = 1 + cos(2π) = 1 + 1 = 2.
b) Se 𝑝 = −1, 𝑞 = 2, 𝑟 = 𝜋 e 𝑠 = 0, então 𝑓(𝑥) = 𝑝 + 𝑞 cos(𝑟𝑥 − 𝑠) => f(x) = -1 + 2.cos(πx - 0) => f(x) = -1 + 2.cos(πx).
Para descobrirmos o valor do período devemos fazer f(x) = f(x + T), onde T é o período:
f(x) = -1 + 2.cos(πx) = f(x + T) = -1 + 2.cos(π.(x + T)) => -1 + 2.cos(πx) = -1 + 2.cos(πx + πT) => 2.cos(πx) = 2.cos(πx + πT) => cos(πx) = cos(πx + πT)
Isto implica em πx = πx + πT ou πx + 2kπ = πx + πT. A primeira alternativa nos remonta a T = 0 o que é trivial, porém, período deve ser diferente de zero.
Na segunda alternativa temos que 2kπ = πT => T = 2k. Como período é o menor número que faz f(x) = f(x + T) acontecer, então, o menor k possível é k = 1 => T = 2.
Então o período é T = 2.
Já a amplitude é obtida fazendo a subtração entre os valores em módulo de máximo e de mínimo da função f(x).
Como f(x) = -1 + 2.cos(πx), fica claro que o maior valor é para x = 2, pois aí πx = 2π e cos(πx) = cos(2π) = 1 => f(xmáx.) = -1 + 2 = 1.
Para mínimo, seria x = 1, por exemplo, pois πx = π => cos(πx) = cos(π) = -1 => f(xmín.) = -1 + 2.cos(πx) = -1 + 2.(-1) = -1 - 2 = -3.
Assim, a amplitude é A = |f(xmáx.) - f(xmín.)| = 4.
c)
Pela figura notamos que o gráfico, por ter influência de um cosseno dado que esta função trigonométrica está presente na expressão de f(x), está deslocado 0,5 para a esquerda.
Também conseguimos notar que o mínimo é -2 e o máximo 3. Então, como o máximo de cos(rx - s) é 1, então f(xmáx) = p + q cos(r.x - s) = p + q = 3.
f(xmín.) = p + q cos(r.x - s) = p - q = -2.
Logo, somando estes dois resultados acima: 2p = 1 => p = 1/2 e q = 5/2.
A função fica f(x) = 1/2 + (5/2).cos(r.x - s).
Para x = -0,5: f(-0,5) = -2 = 1/2 + (5/2).cos(-0,5r - s) => 1/2 + (5/2).cos(0,5r + s) = -2 => 5cos(0,5r + s) = -5 => cos(0,5r + s) = -1 => 0,5r + s = π.
Para x = 1,5: f(1,5) = 3 = 1/2 + (5/2).cos(1,5r - s) => 5cos(1,5r - s) = 5 => cos(1,5r - s) = 1 => 1,5r - s = 2π.
Por estas duas equações:
2r = 3π => r = 3π / 2 e s = π/4.
SOLUÇÃO: p = 1/2, q = 5/2, r = 3π / 2 e s = π/4.