Questão 70268

FUVEST
  1. Matemática
  2. Matemática

(FUVEST - 2022 - 2ª fase)

Uma pirâmide 𝐏 tem base quadrada A_0B_0C_0D_0 de lado medindo 1 𝑢. 𝑚., apoiada em um plano Pi, e quatro faces que são triângulos equiláteros, ligando a base ao ápice E_0 de 𝐏. Os dezesseis pontos A_1A_2A_3B_1B_2B_3C_1C_2C_3D_1D_2D_3E_1E_2E_3 e E_4, indicados na figura, dividem cada aresta da pirâmide em três segmentos de igual medida.

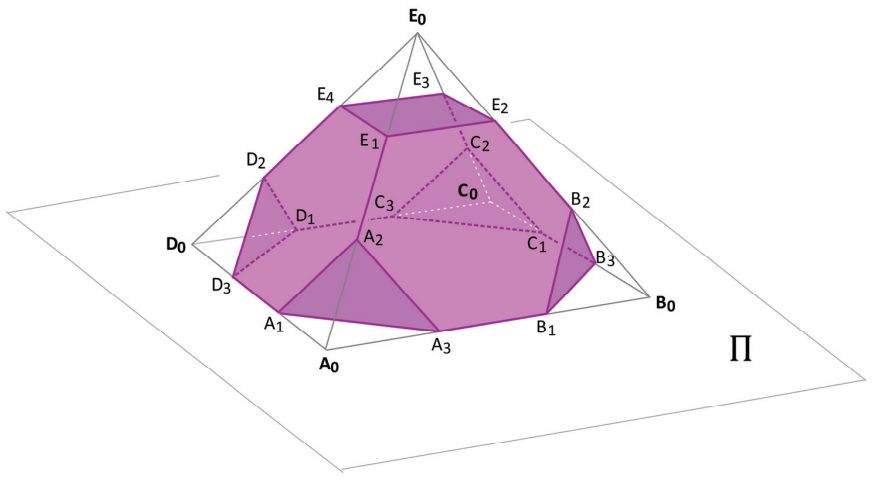
Um novo sólido 𝐒, em destaque na figura, é produzido subtraindo-se de 𝐏 as cinco pirâmides A_0A_1A_2A_3, B_0_1B_2B_3, C_0C_1C_2C_3, D_0 D_1D_2D_3 e E_0E_1E_2E_3. Determine:

 

a) o perímetro da face de 𝐒 que se apoia em Pi, cujos vértices são A_1, A_3, B_1, B_3, C_1, C_3, D_1 e D_3.
b) o volume de 𝐒.
c) a distância entre A_1 e E_2. 

Gabarito:

Resolução:

A) Temos a seguinte figura:

Para o perímetro temos 4 lados que estão no quadrado original que medem frac{1}{3} e 4 lados que são hipotenusas de triângulos retângulos

Medida da hipotenusa: sqrt{2} cdot frac{1}{3}=frac{sqrt{2}}{3}

Perímetro:

S=4cdot frac{sqrt{2}}{3} +4cdot frac{1}{3}

S=frac{4(sqrt{2}+1)}{3} u. m.

B) i) Volume da pirâmide antes dos cortes:

Todos os arestas medem 1 u.m. Podemos utilizar a fórmula do volume de um tetraedro regular:

V=frac{l^3sqrt{2}}{12}

V=frac{sqrt{2}}{12}

ii) Volume de cada uma das quatro pirâmides cortadas da base:

a=frac{1}{3}cdot frac{dsqrt{3}}{2}

Como d=frac{sqrt{2}}{3}: 

a=frac{sqrt{3}}{6}cdot frac{sqrt{2}}{3}

a=frac{sqrt{6}}{18}

Por Pitágoras:

frac{1}{9}=h^2+a^2

h^2=frac{1}{9}-frac{6}{324}

h^2=frac{1}{9}-frac{1}{54}

h^2=frac{5}{54}

h=frac{sqrt{5}}{3sqrt{6}}

O volume de cada pirâmide é área da base vezes altura:

v_1=A_b cdot h

v_1=frac{(frac{sqrt{2}}{3})^2sqrt{3}}{4}cdot frac{sqrt{5}}{3sqrt{6}}

v_1=frac{sqrt{5}}{54sqrt{2}}

iii) Volume da pirãmide cortada superiormente. que é um tetraedro regular de lado frac{1}{3}

v_2=frac{l^3sqrt{2}}{12}

v_2=frac{sqrt{2}}{12cdot 27}

iii) Volume de S:

V_S=frac{sqrt{2}}{12}-4cdot frac{sqrt{5}}{54sqrt{2}}-frac{sqrt2}{324}

V_S=frac{sqrt{2}}{12}-frac{2sqrt{10}}{54}-frac{sqrt2}{324}

V_S=frac{27sqrt{2}-12sqrt{10}-sqrt2}{324}

V_S=frac{26sqrt{2}-12sqrt{10}}{324}

V_S=frac{13sqrt{2}-6sqrt{10}}{162} u.v.

C) Num sistema de coordenadas em três dimensões, em que a origem é o ponto A_0, vamos descobrir as coordenadas de cada ponto.

A_1=(frac{1}{3},0,0)

E_2=(frac{1}{3},frac{2}{3},z)    → somente a altura deste ponto não é clara pela figura, devemos analisar por semelhança de figuras

Se a altura total da pirâmide é h=frac{sqrt{5}}{3sqrt{6}} e o lado da base mede 1, então a pirâmide superior, cuja base mede frac{1}{3} tem altura z:

frac{frac{1}{3}}{1}=frac{z}{h}

z=frac{h}{3}

z=frac{sqrt{5}}{9sqrt{6}}

Ponto E_2=(frac{1}{3},frac{2}{3},frac{sqrt{5}}{9sqrt{6}})

Vamos calcular a distância entre eles pela fórmula:

d^2=(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2

d^2=(0)^2+(frac{2}{3})^2+(frac{sqrt{5}}{9sqrt{6}})^2

d^2=frac{4}{9}+frac{5}{81 cdot 6}

d^2=frac{216+5}{486}

d^2=frac{221}{486}

d=sqrt{frac{221}{486}} u.m.



Questão 1779

FUVEST
  1. Português
  2. Português

(FUVEST - 2016 - 1ª FASE)

No contexto do cartum, a presença de numerosos animais de estimação permite que o juízo emitido pela personagem seja considerado

Ver questão

Questão 1780

FUVEST
  1. Português
  2. Português

(FUVEST - 2016 - 1ª FASE)

Para obter o efeito de humor presente no cartum, o autor se vale, entre outros, do seguinte recurso:

Ver questão

Questão 1794

FUVEST
  1. Português
  2. Português

(Fuvest 2016)

Omolu espalhara a bexiga na cidade. Era uma vingança contra a cidade dos ricos. Mas os ricos tinham a vacina, que sabia Omolu de vacinas? Era um pobre deus das florestas d’África. Um deus dos negros pobres. Que podia saber de vacinas? Então a bexiga desceu e assolou o povo de Omolu. Tudo que Omolu pôde fazer foi transformar a bexiga de negra em alastrim, bexiga branca e tola. Assim mesmo morrera negro, morrera pobre. Mas Omolu dizia que não fora o alastrim que matara. Fora o 1lazareto. Omolu só queria com o alastrim marcar seus filhinhos negros. O lazareto é que os matava. Mas as macumbas pediam que ele levasse a bexiga da cidade, levasse para os ricos latifundiários do sertão. Eles tinham dinheiro, léguas e léguas de terra, mas não sabiam tampouco da vacina. O Omolu diz que vai pro sertão. E os negros, os ogãs, as filhas e pais de santo cantam:

Ele é mesmo nosso pai
e é quem pode nos ajudar...

Omolu promete ir. Mas para que seus filhos negros não o esqueçam avisa no seu cântico de despedida:

Ora, adeus, ó meus filhinhos,
Qu’eu vou e torno a vortá...

E numa noite que os atabaques batiam nas macumbas, numa noite de mistério da Bahia, Omolu pulou na máquina da Leste Brasileira e foi para o sertão de Juazeiro. A bexiga foi com ele.

Jorge Amado, Capitães da Areia.

1lazareto: estabelecimento para isolamento sanitário de pessoas atingidas por determinadas doenças.

Costuma-se reconhecer que Capitães da Areia pertence ao assim chamado “romance de 1930”, que registra importantes transformações pelas quais passava o Modernismo no Brasil, à medida que esse movimento se expandia e diversificava. No excerto, considerado no contexto do livro de que faz parte, constitui marca desse pertencimento

Ver questão

Questão 1804

FUVEST
  1. Português
  2. Português

(Fuvest 2012)

Como não expressa visão populista nem elitista, o livro não idealiza os pobres e rústicos, isto é, não oculta o dano causado pela privação, nem os representa como seres desprovidos de vida interior; ao contrário, o livro trata de realçar, na mente dos desvalidos, o enlace estreito e dramático de limitação intelectual e esforço reflexivo. 

Essas afirmações aplicam-se ao modo como, na obra:

Ver questão