Questão 32985
INSPER
(INSPER - 2016)
A figura acima representa os gráficos das funções
- f(x) = sen(x)
- g(x) = cos(x)
- h(x) = cos(2x)
definidas no intervalo [0,2].
Sabendo que , determine o valor máximo de d(x) = h(x) - g(x).
-0,5
0
1
1,5
2
Gabarito:
2
Resolução:
SOLUÇÃO DESCONSIDERANDO O GRÁFICO:
Temos que h(x) = cos(2x) = cos2x - sen2x, chamando sen2x de 1 - cos2x (da relação fundamental sen2x + cos2x = 1), obtemos h(x) = 2cos2x - 1.
Portanto:
d(x) = h(x) - g(x) = cos(2x) - cos(x) = 2cos2x - 1 - cosx => d(x) = (cosx)2 . 2 - (cosx) - 1.
Chamando cosx de k, temos que d(x) = 2k2 - k - 1. Isto acaba sendo uma equação do segundo grau em k.
Lembrando de equações do segundo grau, perceba que esta equação possui um coeficiente que acompanha o parâmetro de maior expoente, que é o k2, maior que zero (este coeficiente é o a da representação de ax2 + bx + c que nessa função d(x) é o 2 que acompanha o k2). Isto significa que essa parábola é virada para cima (como um sorriso) no plano cartesiano considerado. Logo, a mínima de d(x) seria o vértice dessa parábola:
xVértice = -b/2a = -(-1) / 2.(2) = 1/4, ou seja, o mínimo dessa função ocorre para quando k = cos(x) = 1/4.
Porém, não estamos interessados no mínimo dessa função, mas no máximo.
Lembre-se sempre que o k = cos(x) de d(x) = 2k2 - k - 1 só assume valores reais entre -1 e 1, ou seja, essa parábola está definida para valores de abscissas iguais a k entre -1 e 1. Fazendo Bháskara descobrimos que as raízes de d(x) acontecem para k = -1/2 e k = 1. Então, pelo que sabemos até agora é que o menor valor desta parábola é para k = 1/4, quando k = 1, que é o maior valor que k pode assumir, d(x) = 0, dado que esta é uma raiz, e que quando k = -1/2, d(x) também é igual a zero. Veja a figura abaixo representando essa parábola:
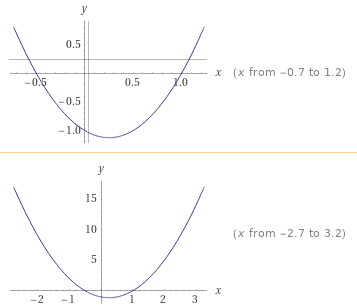
Entre k = -1/2 e k = 1 o gráfico da parábola está em territórios negativos, ou seja, d(x) possui valores negativos. Porém, para k < -1/2, ou seja, para valores de k entre -1 e -1/2 a parábola sobe muito levando d(x) para valores positivos cada vez maiores à medida que diminuimos o valor de k de -1/2 para -1.
Assim, é possível perceber que o maior valor de d(x) será obtido para quando k for igual a -1:
d(x) = 2k2 - k - 1 = 2.(-1)2 - (-1) - 1 = 2 + 1 - 1 = 2.
O maior valor é d(x) = 2.
SOLUÇÃO CONSIDERANDO O GRÁFICO:
Para d(x) = h(x) - g(x) = cos(2x) - cos(x). Vamos primeiramente identificar qual curva representa qual função.
A função seno possui valor nulo para ângulos nulos. A única curva que tem essa propriedade é a curva cinza cheia (veja que lá quando y = 0 e x = 0 ela é a única presente). Logo, a curva cinza representa f(x) = sen(x).
As duas outras curvas devem representar cos(2x) e cos(x). Para x = π, cos(2x) deve ser igual a cos(2π) = 1 e cos(x) deve ser igual a cos(π) = -1. A única curva que possui valor y = 1 para x = π é a curva preta cheia. Logo, a curva preta cheia representa h(x) = cos(2x) e a curva tracejada representa g(x) = cos(x).
Então a função d(x) será uma função cujos valores são obtidos a partir da subtração dos valores em y da curva preta pelos valores em y da curva tracejada, para um mesmo x. Logo, nos pontos em x, ou seja, nos ângulos, em que há maior distância entre a curva preta da curva tracejada é que podemos dizer que é representado o máximo da função. Isto porque como estamos subtraindo os valores das duas curvas, quanto mais separada elas forem melhor.
Veja que isto ocorre para quando x = π. Ali, a curva preta está em y = 1 e a curva tracejada está em y = -1. Fazendo a subtração dessas duas curvas obtemos:
d(x) = h(x) - g(x) = 1 - (-1) = 1 + 1 = 2.
O valor máximo da função d(x) é 2.

