GuruGuia

Questão 36360

FUVEST

(FUVEST 2017 - 2 FASE)

Um quadriculado é formado por n x n quadrados iguais, conforme ilustrado para n = 2 e n = 3. Cada um desses quadrados será pintado de azul ou de branco. Dizemos que dois quadrados Q₁ e Q₂ do quadriculado estão conectados se ambos estiverem pintados de azul e se for possível, por meio de movimentos horizontais e verticais entre quadrados adjacentes, sair de Q₁ e chegar a Q₂ passando apenas por quadrados pintados de azul.

a) Se n = 2, de quantas maneiras distintas será possível pintar o quadriculado de modo que o quadrado Q₁ do canto inferior esquerdo esteja conectado ao quadrado Q₂ do canto superior direito?

b) Suponha que n = 3 e que o quadrado central esteja pintado de branco. De quantas maneiras distintas será possível pintar o restante do quadriculado de modo que o quadrado Q₁ do canto superior esquerdo esteja conectado ao quadrado Q₂ do canto superior direito?

c) Suponha que n = 3. De quantas maneiras distintas será possível pintar o quadriculado de modo que o quadrado Q₁ do canto superior esquerdo esteja conectado ao quadrado Q₂ do canto superior direito?

Gabarito:

Resolução:

Com n=2 para que Q₁ e Q₂ estejam conectados, eles necessariamente devem estar pintados de azul e as outras duas casas possíveis podem estar pintadas de azul ou branco, mas desde que uma delas esteja pintada de azul. Logo, temos:

Somente uma opção para Q₁ e Q₂ e duas opções para as duas casas restantes:

$1 imes1 imes2 imes2=4$

Dessas possibilidades, temos que tirar a que ambas as casas são pintadas de branco. Logo temos: $4-1=3$ possibilidades.

_____________________________________________

Com n=3 e a casa central pintada de branco, temos que analisar duas situações: quando a segunda casa da primeira linha é azul e quando ela é branca.

Quando é branca, a única forma de se conectar Q₁ e Q₂é com as demais casas pintadas de azul:

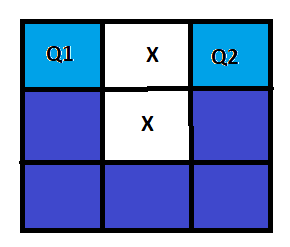
Logo, só temos uma forma de pintá-las nesse caso.

Quando a segunda casa da primeira linha é azul, não importa a cor das demais casas, já que Q₁ e Q₂já estarão conectados. Sendo assim:

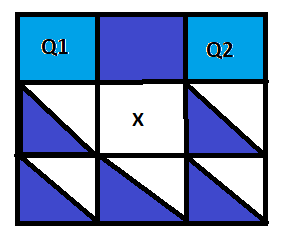
Temos 2 opções para cada uma das 5 casas. Assim, o número de formas diferentes de se pintar o quadriculado é:

$2 imes2 imes2 imes2 imes2=2^5=32$

Logo, como temos 32 + 1 = 33 formas diferentes de se pintar conectando Q₁ e Q₂.

_________________________________________

Primeiro, analisando o caso em que a casa entre Q₁ e Q₂é necessariamente azul, temos:

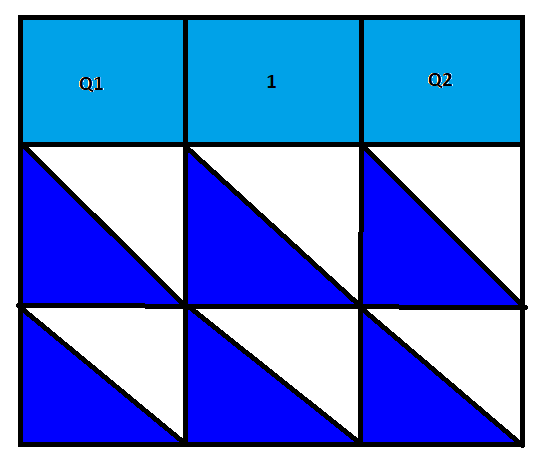
Nesse caso, como Q₁ e Q₂já estão conectados, as outras casas podem ter qualquer cor. Portanto:

$2 imes2 imes2 imes2 imes2 imes2=2^6=64$ formas distintas.

Caso a casa entre Q₁ e Q₂esteja branca, temos as seguintes opções:

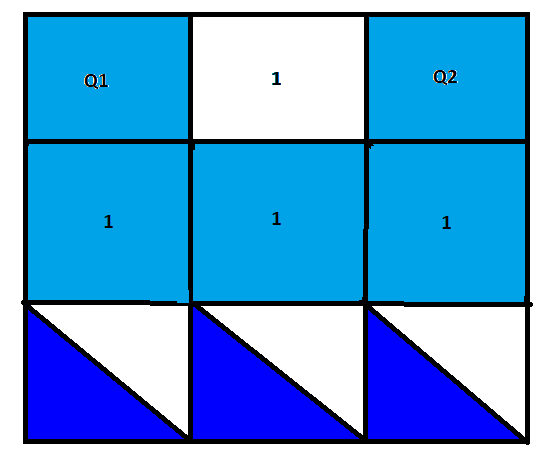
Com a casa central azul, necessariamente as casas abaixo de Q₁ e Q₂devem também ser azuis, mas as 3 casas inferiores podem ter qualquer cor (já que Q₁ e Q₂já estarão conectados pela linha do meio).

Logo, temos:

$2 imes2 imes2=2^3=8$ formas distintas.

Por fim, caso a casa central seja branca, temos somente uma opção possível (como foi abordado no item b):

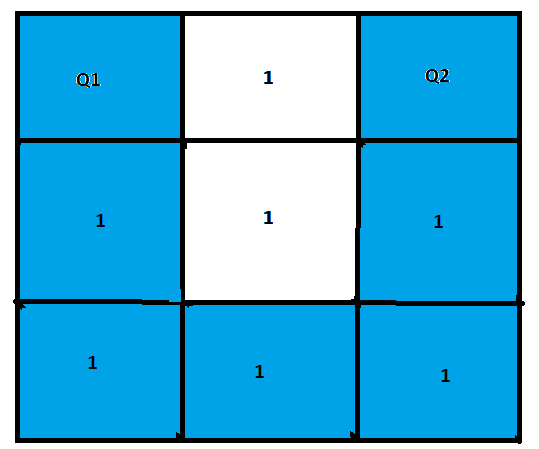
Sendo assim, temos $64+8+1=73$ formas distintas.

Questão 1779

FUVEST

(FUVEST - 2016 - 1ª FASE)

No contexto do cartum, a presença de numerosos animais de estimação permite que o juízo emitido pela personagem seja considerado

Ver questão

Questão 1780

FUVEST

(FUVEST - 2016 - 1ª FASE)

Para obter o efeito de humor presente no cartum, o autor se vale, entre outros, do seguinte recurso:

Ver questão

Questão 1794

FUVEST

(Fuvest 2016)

Omolu espalhara a bexiga na cidade. Era uma vingança contra a cidade dos ricos. Mas os ricos tinham a vacina, que sabia Omolu de vacinas? Era um pobre deus das florestas d’África. Um deus dos negros pobres. Que podia saber de vacinas? Então a bexiga desceu e assolou o povo de Omolu. Tudo que Omolu pôde fazer foi transformar a bexiga de negra em alastrim, bexiga branca e tola. Assim mesmo morrera negro, morrera pobre. Mas Omolu dizia que não fora o alastrim que matara. Fora o¹lazareto. Omolu só queria com o alastrim marcar seus filhinhos negros. O lazareto é que os matava. Mas as macumbas pediam que ele levasse a bexiga da cidade, levasse para os ricos latifundiários do sertão. Eles tinham dinheiro, léguas e léguas de terra, mas não sabiam tampouco da vacina. O Omolu diz que vai pro sertão. E os negros, os ogãs, as filhas e pais de santo cantam:

Ele é mesmo nosso pai
e é quem pode nos ajudar...

Omolu promete ir. Mas para que seus filhos negros não o esqueçam avisa no seu cântico de despedida:

Ora, adeus, ó meus filhinhos,
Qu’eu vou e torno a vortá...

E numa noite que os atabaques batiam nas macumbas, numa noite de mistério da Bahia, Omolu pulou na máquina da Leste Brasileira e foi para o sertão de Juazeiro. A bexiga foi com ele.

Jorge Amado, Capitães da Areia.

¹lazareto: estabelecimento para isolamento sanitário de pessoas atingidas por determinadas doenças.

Costuma-se reconhecer que Capitães da Areia pertence ao assim chamado “romance de 1930”, que registra importantes transformações pelas quais passava o Modernismo no Brasil, à medida que esse movimento se expandia e diversificava. No excerto, considerado no contexto do livro de que faz parte, constitui marca desse pertencimento

Ver questão

Questão 1804

FUVEST

(Fuvest 2012)

Como não expressa visão populista nem elitista, o livro não idealiza os pobres e rústicos, isto é, não oculta o dano causado pela privação, nem os representa como seres desprovidos de vida interior; ao contrário, o livro trata de realçar, na mente dos desvalidos, o enlace estreito e dramático de limitação intelectual e esforço reflexivo.

Essas afirmações aplicam-se ao modo como, na obra:

Ver questão