GuruGuia

Questão 61483

UNIT

(UNIT-AL - 2019) Uma clínica verificou que, no grupo de pacientes atendidos durante o ano de 2018, 50% deles foram afetados pela doença X, 45% foram afetados pela doença Y, 49% foram afetados pela doença Z, 15% foram afetados pelas doenças X, Y e Z, 20% foram afetados pelas doenças X e Y, 24% foram afetados pelas doenças Y e Z e 25% foram afetados pelas doenças X e Z. A porcentagem de doentes afetados por apenas uma dessas doenças foi de

25%

51%

75%

144%

228%

Gabarito:

51%

Resolução:

Podemos preencher um diagrama de Venn com as informações dadas realizando as subtrações adequadas:

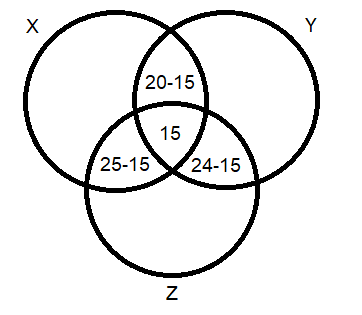
Realizando as subtrações:

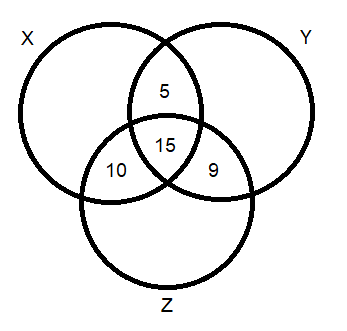
Continuando:

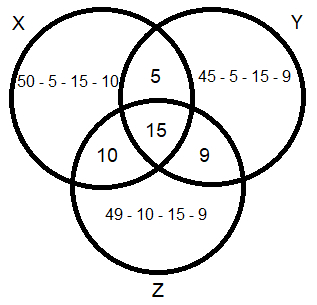
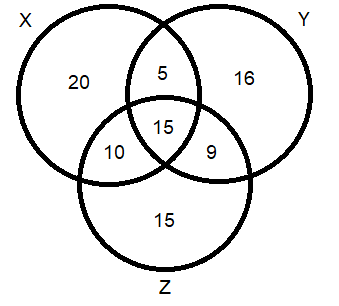
Neste ponto, já temos todas as informações dos conjuntos bem simplificadas, poderiamos até descobrir quantos pacientes não tem nenhuma doença. Porém o enunciado pede apenas a porcentagem de pacientes que apresentam apenas uma doença, ou seja, a soma dos pacientes que estão só em X, só em Y e só em Z:

$20 + 16 + 15 = 51\%$

Alternativa B.

Questão 32237

UNIT

Considerando-se a PA (131, 124, 117, ... ,−2), pode-se concluir que a soma dos seus termos corresponde a

Ver questão

Questão 32249

UNIT

Se o termo geral de uma sequência é $a_{n} = -2n + frac{1}{2},, ngeq 1$ , então o seu terceiro termo é

Ver questão

Questão 61371

UNIT

(UNIT-AL - 2019) Em uma determinada atividade no Ensino Médio, os alunos construíram uma célula eucariótica e utilizou a escala numérica de 100:1. Lembrando-se que, na escala numérica, as unidades são indicadas sempre em centímetros. Supondo-se que a célula construída tenha 10 centímetros de largura e 50 centímetros de comprimento, a medida real dessa célula, em centímetros, de acordo com a escalautilizada, seria, respectivamente,

Ver questão

Questão 61479

UNIT

(UNIT-AL - 2019) Analisando as proposições a seguir, identifique com V as verdadeiras e com F, as falsas.

( ) Se $M = mathbb{Q} cap mathbb{R}$ e $N = mathbb{I} - mathbb{Q}$ , tem-se que $M cup N = mathbb{R}$ .
( ) Se $n(G) = 42$ , $n(H) = 36$ e $n(G cap H) = 12$ , com isso $n(Gcup H) = 66$ .
( ) Se $T = {0, 2, 4, 6}$ , $P = {1, 2}$ , $Q = {2, 3, 4}$ e $S = {4}$ então $(T - P)cap (Q cup S) = {3, 4, 5}$ .
( ) Todo número inteiro é racional, mas nem todo número racional é inteiro.

A alternativa que contém a sequência correta, de cima para baixo, é a

Ver questão