Questão 59445
FUVEST
(FUVEST 2021 - 1ª fase)
Três triângulos equiláteros e dois quadrados formam uma figura plana, como ilustrado. Seus centros são os vértices de um pentágono irregular, que está destacado na figura. Se T é a área de cada um dos triângulos e Q a área de cada um dos quadrados, a área desse pentágono é
T + Q.
1/2 T + 1/2 Q.
T + 1/2 Q.
1/3 T + 1/4 Q.
1/3 T + 1/2 Q.
Gabarito:
T + 1/2 Q.
Resolução:
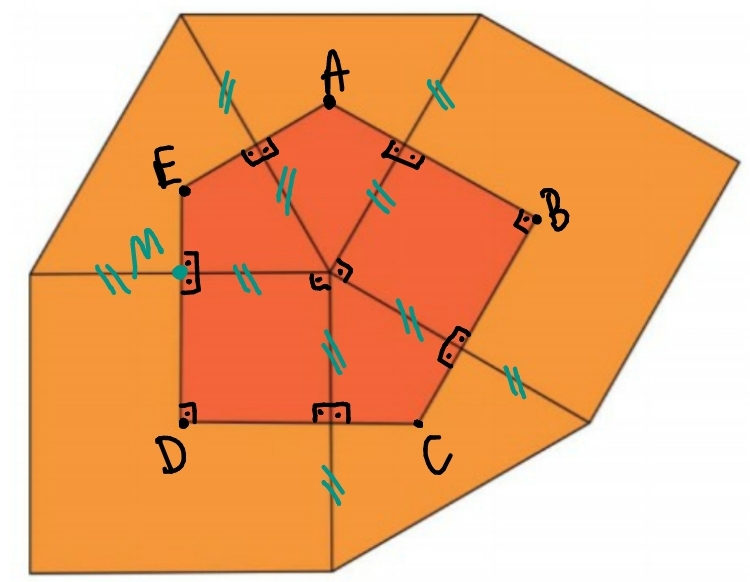
Como o objeto do centro se trata de um pentágono, então os segmentos AB, BC, CD e EA se tratam dos lados do pentágono ABCDE.
Se D é o centro do quadrado e E é o centro de um dos triângulos e como o lado superior do quadrado é igual ao lado inferior do triângulo, ao conectar os pontos D e E obtemos um segmento, ED, que passa pelo ponto médio do lado em comum ao quadrado e ao triângulo e que é também perpendicular a este lado em comum. Isto acontece porque ao conectarmos o centro E do triângulo ao ponto médio do lado inferior (que aqui podemos chamar de M) obtemos o segmento EM, mas como M também é o ponto médio do lado superior do quadrado de centro D, DM também é um semgento médio do quadrado. Logo, ED é um segmento que é a junção de dois segmentos médios do triângulo e do quadrado.
Devemos lembrar agora que em um triângulo equilátero, o segmento médio de um dos lados do triângulo é congruente à altura e à bissetriz em relação a esse lado do triângulo. Logo, o segmento EM é perpendicular ao lado em comum ao quadrado. E é trivial reconhecer que o segmento DM também é perpendicular a esse lado dado que ED é um lado de um pentágono.
Agora com esta prova em mãos, podemos estender esse conhecimento a todos os outros lados do pentágono. Agora note o seguinte: o lado DM é a metade do lado do quadrado. Logo, o quadrado vermelho mais escuro, dentro do quadrado maior, é um quadrado de lado igual à metade do lado do quadrado maior. Dessa forma, a área desse quadrado menor é igual à 1/4 da área do quadrado maior.
Logo, a área do quadrado menor é igual a 1/4 de Q.
Já a área mais avermelhada dentro dos triângulos pode ser obtida fazendo a seguinte observação:
Aqui dividimos essa área em duas, Área I e Área II. Porém, veja que, por simetria, essas duas áreas são iguais. Também tenha em mente a propriedade de alturas em triângulos equiláteros em que o centro do triângulo ou ortocentro do triângulo equilátero divide a altura desse triângulo em duas partes, uma parte com comprimento igual a 2/3 da altura e o outro comprimento com comprimento igual a 1/3 da altura. Logo, o comprimento do segmento do lado e superior da figura acima equivale a 1/3 da altura desses triângulos.
Chamando de 2x o lado desses triângulos, temos que os lados inferior e da direita da figura acima, por se tratarem da metade dos lados do triângulo, possuem comprimentos iguais a x.
Desta forma:
Área I:
Como a Área II é igual a Área I, então:
A área total dessa figura (mais avermelhada pertencentes aos triângulos) é igual a:
Porém, qual é a área desses triângulos?
Logo:
Logo, por simetria, todas as áreas mais avermelhadas que pertencem aos triângulos possuem área igual a 1/3 T.
Desta forma, podemos descobrir a área total do pentágono pela soma:
áreas pertencentes aos triângulos:1/3 T + 1/3 T + 1/3 T = T
áreas pertencentes aos quadrados: 1/4 Q + 1/4 Q = 1/2 Q
Soma total = área do pentágono = T + 1/2 Q.
A alternativa correta é a Letra E.