GuruGuia

Questão 60252

FUVEST

(FUVEST - 2021 - 2ª FASE)

Um plano de inclinação θ situa-se sobre uma mesa horizontal de altura 4h, conforme indicado na figura. Um carrinho de massa m parte do repouso no ponto A, localizado a uma altura h em relação à superfície da mesa, até atingir o ponto B na parte inferior do plano para então executar um movimento apenas sob a ação da gravidade até atingir o solo a uma distância horizontal D da base da mesa, conforme mostra a figura. Ao utilizarmos rampas com diferentes inclinações θ (com o carrinho sempre partindo de uma mesma altura h), obtemos diferentes alcances horizontais D.

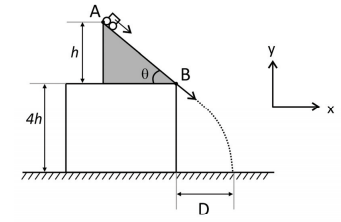
a) Calcule o intervalo de tempo decorrido entre a partida do carrinho, situado inicialmente no topo do plano inclinado, até atingir o solo, considerando o valor para a inclinação θ = 90º.

b) Usando a conservação da energia mecânica e supondo agora uma inclinação θ qualquer, obtenha o módulo do vetor velocidade |𝑣⃑| com que o carrinho deixa a superfície do plano inclinado.

c) Encontre o valor do alcance D supondo que a inclinação do plano seja de θ = 45º.

Note e adote: Considere conhecido o módulo 𝑔 da aceleração da gravidade. Despreze o efeito de forças dissipativas.

Gabarito:

Resolução:

a)Quando θ = 90º o carrinho irá cair apenas verticalmente, por influência da gravidade, percorrendo 5h até chegar ao solo.

$S = S_0 + V_0cdot t + frac{acdot t^2}{2}.$

$0 = 5h + 0cdot t -frac{gcdot t^2}{2}.$

$t = sqrt{frac{10h}{g}}.$

b) Estabelecendo o potencial gravitacional nulo na posição y = 4h e a origem do eixo vertical no solo, teremos a energia mecânica inicial igual a mgh, dado que partimos do repouso.

Enquanto na posição y = 4h haverá apenas energia cinética cujo módulo é dado por $K = frac{m|vec{v}|^2}{2}$

Pensando na conservação da energia mecânica podemos escrever que:

$mgh = frac{m|vec{v}|^2}{2}$

Assim: $|vec{v}| = sqrt{2gh}.$

c) Supondo agora uma inclinação $heta = 45^circ.$

O nosso alcance será encontrado a partir da relação D = v_xt, em que t é o tempo de queda que será encontrado do movimento na vertical e v_x é a componente da velocidade na direção x.

Do movimento na vertical que é uniformemente variado teremos:

$0 = 4h - |vec{v}|cos(45^circ)cdot t - frac{gt^2}{2}.$

Da análise anterior temos $|vec{v}| = sqrt{2gh}$ .

Então $0 = 4h - frac{sqrt{2gh}cdotsqrt{2}cdot t}{2} - frac{gt^2}{2}$ .

$0 = frac{-gt^2}{2} - sqrt{gh}cdot t + 4h.$

$t = frac{sqrt{gh}pm sqrt{gh +8gh}}{-g}$

Queremos um valor positivo para t, então precisamos pegar o numerador negativo:

$t = frac{sqrt{gh}- sqrt{9gh }}{-g}$

$t = 2sqrtfrac{h}{g}$ .

Dessa forma teremos o nosso alcance dado por:

$D = |vec{v}|sen45^circcdot t = sqrt{gh}*2sqrt{frac {h}{g}}$

$D = 2h.$

Questão 1779

FUVEST

(FUVEST - 2016 - 1ª FASE)

No contexto do cartum, a presença de numerosos animais de estimação permite que o juízo emitido pela personagem seja considerado

Ver questão

Questão 1780

FUVEST

(FUVEST - 2016 - 1ª FASE)

Para obter o efeito de humor presente no cartum, o autor se vale, entre outros, do seguinte recurso:

Ver questão

Questão 1794

FUVEST

(Fuvest 2016)

Omolu espalhara a bexiga na cidade. Era uma vingança contra a cidade dos ricos. Mas os ricos tinham a vacina, que sabia Omolu de vacinas? Era um pobre deus das florestas d’África. Um deus dos negros pobres. Que podia saber de vacinas? Então a bexiga desceu e assolou o povo de Omolu. Tudo que Omolu pôde fazer foi transformar a bexiga de negra em alastrim, bexiga branca e tola. Assim mesmo morrera negro, morrera pobre. Mas Omolu dizia que não fora o alastrim que matara. Fora o¹lazareto. Omolu só queria com o alastrim marcar seus filhinhos negros. O lazareto é que os matava. Mas as macumbas pediam que ele levasse a bexiga da cidade, levasse para os ricos latifundiários do sertão. Eles tinham dinheiro, léguas e léguas de terra, mas não sabiam tampouco da vacina. O Omolu diz que vai pro sertão. E os negros, os ogãs, as filhas e pais de santo cantam:

Ele é mesmo nosso pai
e é quem pode nos ajudar...

Omolu promete ir. Mas para que seus filhos negros não o esqueçam avisa no seu cântico de despedida:

Ora, adeus, ó meus filhinhos,
Qu’eu vou e torno a vortá...

E numa noite que os atabaques batiam nas macumbas, numa noite de mistério da Bahia, Omolu pulou na máquina da Leste Brasileira e foi para o sertão de Juazeiro. A bexiga foi com ele.

Jorge Amado, Capitães da Areia.

¹lazareto: estabelecimento para isolamento sanitário de pessoas atingidas por determinadas doenças.

Costuma-se reconhecer que Capitães da Areia pertence ao assim chamado “romance de 1930”, que registra importantes transformações pelas quais passava o Modernismo no Brasil, à medida que esse movimento se expandia e diversificava. No excerto, considerado no contexto do livro de que faz parte, constitui marca desse pertencimento

Ver questão

Questão 1804

FUVEST

(Fuvest 2012)

Como não expressa visão populista nem elitista, o livro não idealiza os pobres e rústicos, isto é, não oculta o dano causado pela privação, nem os representa como seres desprovidos de vida interior; ao contrário, o livro trata de realçar, na mente dos desvalidos, o enlace estreito e dramático de limitação intelectual e esforço reflexivo.

Essas afirmações aplicam-se ao modo como, na obra:

Ver questão