GuruGuia

Questão 78791

FUVEST

(FUVEST - 2023)

Considere as circunferências $C,C_{1},C_{2},C_{3},...,C_{n},...$ e a reta s satisfazendo as seguintes propriedades:

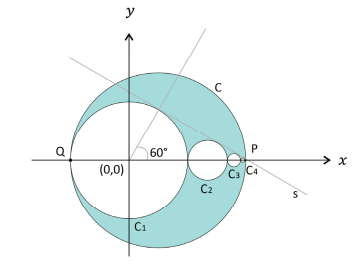
• A circunferência $C_{1}$ tem centro (0,0) e raio $r=4$ . Os centros das demais circunferências pertencem ao eixo $Ox$ .

• A circunferência $C_{2}$ é tangente a $C_{1}$ e a $C_{3}$ , a circunferência $C_{3}$ é tangente a $C_{2}$ e a $C_{4}$ , e assim por diante.

• A reta s é tangente a cada circunferência $C_{n}$ para $ngeq 1$ .

• O segmento que liga o centro de $C_{1}$ ao ponto em que s tangencia $C_{1}$ forma um ângulo de 60° com o eixo $Ox$ .

• A circunferência C é tangente a $C_{1}$ no ponto $Q = (-4,0)$ e passa pelo ponto $P= (x_{0},0)$ .

Com base nessas informações,

a) determine o raio da circunferência C.

b) dado $ngeq 1$ , determine a razão entre os raios das circunferências consecutivas $C_{n+1}$ e $C_{n}$ .

c) determine a área da região sombreada na figura.

Gabarito:

Resolução:

A) determine o raio da circunferência C.

Primeiro vamos colocar no desenho as informações apresentadas:

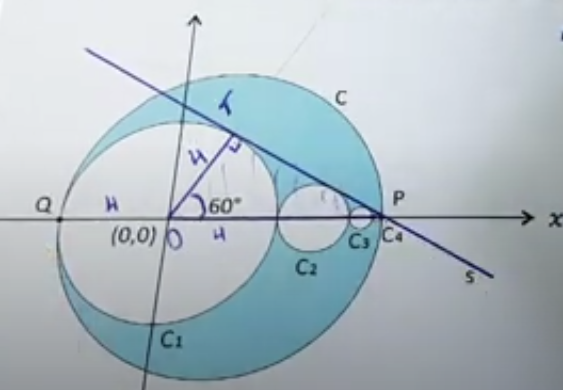
Portanto, temos que o raio da circunferência C é metade de QP

$R_{c} = frac{QP}{2}$

Observando o desenho temos que QP = OP + 4

No triângulo OTP, podemos observar que:

$\ Delta OTP : cos(60) = frac{4}{OP} \ \ frac{1}{2} = frac{4}{OP} \ \ OP = 8$

QP = 8 + 4 = 12

Então temos que o raio da circunferência é:

$R_{c} = frac{12}{2} = 6$

B) Nesse item iremos utilizar semelhando dos triângulos descritos abaixo, a fim de encontrar o raio:

$Delta OTP sim Delta O_{1} T_{1} P_{1}$

$frac{R_{1}}{R_{2}} = frac{OP}{O_{1}P}$

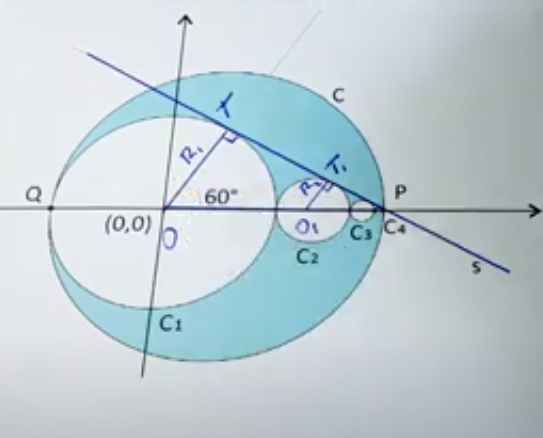
Temos que R1 = 4 e OP = 8 (achamos no item A)

$frac{4}{R_{2}} = frac{8}{O_{1}P}$

Agora vamos analisar o tamanho de O1P , veja o desenho abaixo:

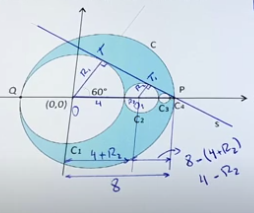
Portanto, temos:

$frac{4}{R_{2}} = frac{8}{4 - R_{2}}$

$8R_{2} = 16 - 4R_{2}$

$R_{2} = frac{4}{3}$

Temos que razão entre os raios, será:

$frac{frac{4}{3}}{4}= frac{1}{3}$

C) Temos que área sombreada será:

$A_{sombreada} = A_{total } - S_{soma infinita das areas}$

$A_{sombreada} = pi r^{2} - S_{infinita}$

Podemos perceber que temos uma PG em relações as áreas da circunferência:

$pi 4^{2} , pi. (frac{4}{3})^{2}$

Temos a razão igual a 1/9

$S_{infinita} = frac{a_{1}}{1- q}$

$S_{infinita} = frac{pi 16}{1- frac{1}{9}} = frac{16 pi}{frac{8}{9}} = 18 pi$

$A_{sombreada} = pi 6^{2} - 18pi = 18 pi$

Questão 1779

FUVEST

(FUVEST - 2016 - 1ª FASE)

No contexto do cartum, a presença de numerosos animais de estimação permite que o juízo emitido pela personagem seja considerado

Ver questão

Questão 1780

FUVEST

(FUVEST - 2016 - 1ª FASE)

Para obter o efeito de humor presente no cartum, o autor se vale, entre outros, do seguinte recurso:

Ver questão

Questão 1794

FUVEST

(Fuvest 2016)

Omolu espalhara a bexiga na cidade. Era uma vingança contra a cidade dos ricos. Mas os ricos tinham a vacina, que sabia Omolu de vacinas? Era um pobre deus das florestas d’África. Um deus dos negros pobres. Que podia saber de vacinas? Então a bexiga desceu e assolou o povo de Omolu. Tudo que Omolu pôde fazer foi transformar a bexiga de negra em alastrim, bexiga branca e tola. Assim mesmo morrera negro, morrera pobre. Mas Omolu dizia que não fora o alastrim que matara. Fora o¹lazareto. Omolu só queria com o alastrim marcar seus filhinhos negros. O lazareto é que os matava. Mas as macumbas pediam que ele levasse a bexiga da cidade, levasse para os ricos latifundiários do sertão. Eles tinham dinheiro, léguas e léguas de terra, mas não sabiam tampouco da vacina. O Omolu diz que vai pro sertão. E os negros, os ogãs, as filhas e pais de santo cantam:

Ele é mesmo nosso pai
e é quem pode nos ajudar...

Omolu promete ir. Mas para que seus filhos negros não o esqueçam avisa no seu cântico de despedida:

Ora, adeus, ó meus filhinhos,
Qu’eu vou e torno a vortá...

E numa noite que os atabaques batiam nas macumbas, numa noite de mistério da Bahia, Omolu pulou na máquina da Leste Brasileira e foi para o sertão de Juazeiro. A bexiga foi com ele.

Jorge Amado, Capitães da Areia.

¹lazareto: estabelecimento para isolamento sanitário de pessoas atingidas por determinadas doenças.

Costuma-se reconhecer que Capitães da Areia pertence ao assim chamado “romance de 1930”, que registra importantes transformações pelas quais passava o Modernismo no Brasil, à medida que esse movimento se expandia e diversificava. No excerto, considerado no contexto do livro de que faz parte, constitui marca desse pertencimento

Ver questão

Questão 1804

FUVEST

(Fuvest 2012)

Como não expressa visão populista nem elitista, o livro não idealiza os pobres e rústicos, isto é, não oculta o dano causado pela privação, nem os representa como seres desprovidos de vida interior; ao contrário, o livro trata de realçar, na mente dos desvalidos, o enlace estreito e dramático de limitação intelectual e esforço reflexivo.

Essas afirmações aplicam-se ao modo como, na obra:

Ver questão