Questão 77096
FUVEST
(FUVEST- 2023 - 1ª fase)
O telescópio espacial James Webb, lançado em dezembro de 2021, move-se nas proximidades de um ponto especial chamado ponto de Lagrange, sobre o qual um objeto orbita o Sol com o mesmo período de translação que a Terra. O esquema a seguir, fora de escala, representa o Sol, a Terra e o telescópio Webb, com as respectivas massas e distâncias indicadas.
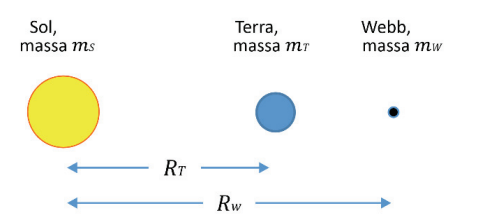
A força resultante necessária para manter um objeto de massa em uma órbita circular de raio
com velocidade angular
é
. Sendo
e
as intensidades das forças gravitacionais resultantes sobre a Terra e sobre o telescópio, respectivamente, assinale a alternativa que descreve a razão
entre essas forças.
Note e adote: Despreze os efeitos gravitacionais da Lua e suponha que seja desprezível frente às outras massas e que as órbitas sejam perfeitamente circulares. Suponha ainda que o telescópio se situe exatamente sobre o ponto de Lagrange.
Gabarito:
Resolução:
A intensidade da força gravitacional na Terra e no Webb é:
Como o período de translação de ambos são iguais:
Alternativa C.