FUVEST 2006

Questão 44933

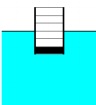
(FUVEST - 2006 - 1 FASE ) Um recipiente cilíndrico vazio flutua em um tanque de água com parte de seu volume submerso, como na figura. Quando o recipiente começa a ser preenchido, lentamente, com água, a altura máxima que a água pode atingir em seu interior, sem que ele afunde totalmente, é melhor representada por

Questão 44934

(FUVEST - 2006 - 1 FASE ) Duas hastes, A e B, movendo-se verticalmente, produzem ondas em fase, que se propagam na superfície da água, com mesma freqüência f e período T, conforme a figura. No ponto P, ponto médio do segmento AB, uma bóia sente o efeito das duas ondas e se movimenta para cima e para baixo. O gráfico que poderia representar o deslocamento vertical y da bóia, em relação ao nível médio da água, em função do tempo t, é

Questão 44935

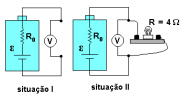
(FUVEST - 2006 - 1 FASE ) Uma bateria possui força eletromotriz ε e resistência interna R₀. Para determinar essa resistência, um voltímetro foi ligado aos dois pólos da bateria, obtendo-se V₀ = ε (situação I). Em seguida, os terminais da bateria foram conectados a uma lâmpada. Nessas condições, a lâmpada tem resistência R = 4 Ω e o voltímetro indica V_A (situação II), de tal forma que V₀/V_A = 1,2. Dessa experiência, conclui-se que o valor de R₀ é

Questão 44940

(FUVEST - 2006) Uma pista de skate, para esporte radical, é montada a partir de duas rampas R₁ e R₂, separadas entre A e B por uma distância D, com as alturas e ângulos indicados na figura. A pista foi projetada de tal forma que um skatista, ao descer a rampa R₁, salta no ar, atingindo sua altura máxima no ponto médio entre A e B, antes de alcançar a rampa R₂.

a) Determine o módulo da velocidade V_A, em m/s, com que o skatista atinge a extremidade A da rampa R₁.

b) Determine a altura máxima H, em metros, a partir do solo, que o skatista atinge, no ar, entre os pontos A e B.

c) Calcule qual deve ser a distância D, em metros, entre os pontos A e B, para que o skatista atinja a rampa R₂ em B, com segurança.

Questão 44941

(FUVEST - 2006) Um gaveteiro, cujas dimensões estão indicadas no corte transversal, em escala, representado nas figuras, possui três gavetas iguais, onde foram colocadas massas de 1 kg, 8 kg e 3 kg, distribuídas de modo uniforme, respectivamente no fundo das gavetas G₁, G₂ e G₃. Quando a gaveta G₂ é puxada, permanecendo aberta, existe o risco de o gaveteiro ficar desequilibrado e inclinar-se para frente

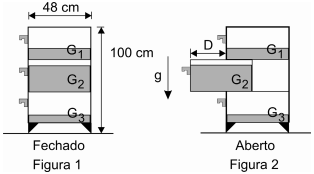
a) Indique, no esquema abaixo, a posição do centro de massa de cada uma das gavetas quando fechadas, identificando esses pontos com o símbolo ×.

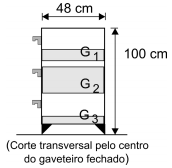
b) Determine a distância máxima D, em cm, de abertura da gaveta G₂ , nas condições da figura 2, de modo que o gaveteiro não tombe para frente.

c) Determine a maior massa M_max , em kg, que pode ser colocada em G₂ , sem que haja risco de desequilibrar o gaveteiro quando essa gaveta for aberta completamente, mantendo as demais condições.

Questão 44942

(FUVEST - 2006) Um elevador de carga, com massa M = 5 000 kg, é suspenso por um cabo na parte externa de um edifício em construção. Nas condições das questões abaixo, considere que o motor fornece a potência P = 150 kW.

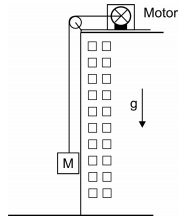
a) Determine a força F₁, em N, que o cabo exerce sobre o elevador, quando ele é puxado com velocidade constante.

b) Determine a força F₂, em N, que o cabo exerce sobre o elevador, no instante em que ele está subindo com uma aceleração para cima de módulo a = 5 m/s₂.

c) Levando em conta a potência P do motor, determine a velocidade V₂, em m/s, com que o elevador estará subindo, nas condições do item (b) (a = 5 m/s² ).

d) Determine a velocidade máxima V_L, em m/s, com que o elevador pode subir quando puxado pelo motor.

Questão 44943

(FUVEST - 2006)  Uma figura gravada em uma folha de plástico (transparência) foi projetada sobre uma parede branca, usando-se uma fonte de luz e uma única lente, colocada entre a folha e a parede, conforme esquema ao lado.

A transparência e a imagem projetada, nas condições de tamanho e distância usadas, estão representadas, em escala, na folha de respostas. As figuras 1 e 2 correspondem a vistas de frente e a figura 3, a vista lateral.

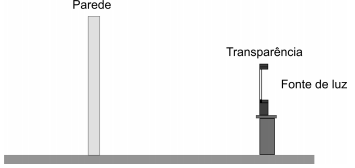
a) Determine, no esquema abaixo, traçando as linhas de construção apropriadas, a posição onde foi colocada a lente, indicando essa posição por uma linha vertical e a letra L. Marque o centro óptico da lente e indique sua posição pela letra C.

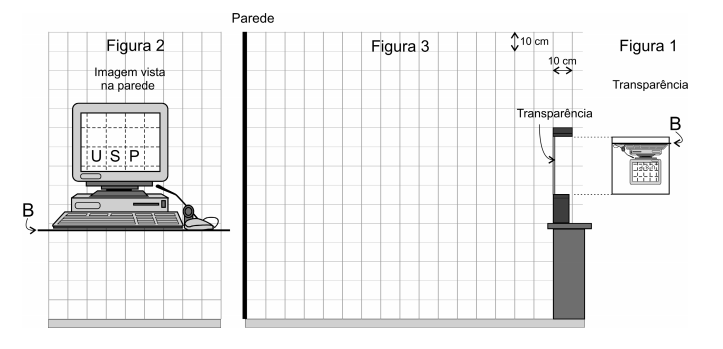
b) Determine graficamente, no esquema da folha de resposta, traçando as linhas de construção apropriadas, a posição de cada um dos focos da lente, indicando suas posições pela letra F.

c) Represente, indicando por B_nova, na figura 2, a posição da linha B, quando o centro óptico da lente for rebaixado em 10 cm (1 quadradinho).

Questão 44944

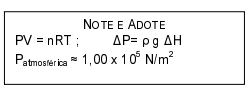
(FUVEST - 2006) Dois tanques cilíndricos verticais, A e B, de 1,6 m de altura e interligados, estão parcialmente cheios de água e possuem válvulas que estão abertas, como representado na figura para a situação inicial. Os tanques estão a uma temperatura T₀ = 280 K e à pressão atmosférica P₀. Em uma etapa de um processo industrial, apenas a válvula A é fechada e, em seguida, os tanques são aquecidos a uma temperatura T₁, resultando na configuração indicada na figura para a situação final.

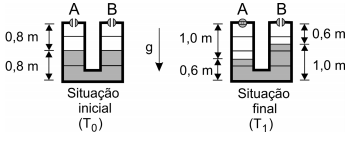
a) Determine a razão R₁ = P₁/P₀, entre a pressão final P₁ e a pressão inicial P₀ do ar no tanque A.

b) Determine a razão R₂ = T₁/T₀, entre a temperatura final T₁ e a temperatura inicial T₀ dentro dos tanques.

c) Para o tanque B, determine a razão R₃ = m₀/m₁ entre a massa de ar m0 contida inicialmente no tanque B e a massa de ar final m1, à temperatura T₁, contida nesse mesmo tanque.

Questão 44945

(FUVEST - 2006) Na época da formação da Terra, estimada como tendo ocorrido há cerca de 4,2 bilhões de anos, os isótopos de Urânio radioativo ²³⁵U e ²³⁸U existiam em maior quantidade, pois, ao longo do tempo, parte deles desintegrouse, deixando de existir como elemento Urânio. Além disso, eram encontrados em proporções diferentes das de hoje, já que possuem meias-vidas diferentes. Atualmente, em uma amostra de 1,000 kg de Urânio, há 0,993 kg de ²³⁸U e 0,007 kg de ²³⁵U, de modo que o ²³⁵U corresponde a 0,7% da massa total e tem importância estratégica muito grande, pela sua utilização em reatores nucleares.

a) Estime a massa M238, em kg, de uma amostra de ²³⁸U, na época da formação da Terra, a partir da qual restaram hoje 0,993 kg de ²³⁸U.

b) Estime, levando em conta o número de meias-vidas do ²³⁵U, a massa M235, em kg, de uma amostra de 235U, na época da formação da Terra, a partir da qual restaram hoje 0,007 kg de ²³⁵U.

c) Estime a porcentagem P em massa de ²³⁵U em relação à massa total de Urânio em uma amostra na época da formação da Terra.

Questão 44946

(FUVEST - 2006) Uma pequena esfera, com carga elétrica positiva Q = 1,5 x 10^-9 C, está a uma altura D = 0,05 m acima da superfície de uma grande placa condutora, ligada à Terra, induzindo sobre essa superfície cargas negativas, como na figura 1. O conjunto dessas cargas estabelece um campo elétrico que é idêntico, apenas na parte do espaço acima da placa, ao campo gerado por uma carga +Q e uma carga -Q, como se fosse uma “imagem” de Q que estivesse colocada na posição representada na figura 2.

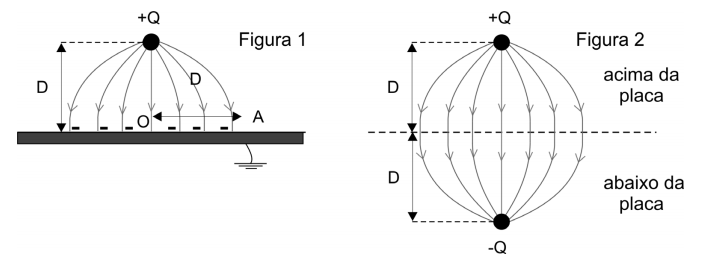
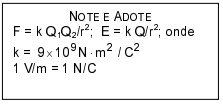
a) Determine a intensidade da força F, em N, que age sobre a carga +Q, devida às cargas induzidas na placa.

b) Determine a intensidade do campo elétrico E₀, em V/m, que as cargas negativas induzidas na placa criam no ponto onde se encontra a carga +Q.

c) Represente, no diagrama abaixo, no ponto A, os vetores campo elétrico e , causados, respectivamente, pela carga +Q e pelas cargas induzidas na placa, bem como o campo resultante, EA r . O ponto A está a uma distância D do ponto O da figura e muito próximo à placa, mas acima dela.

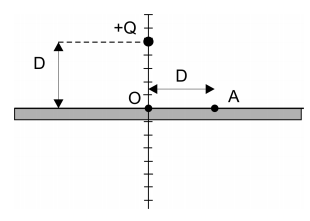
d) Determine a intensidade do campo elétrico resultante E_A, em V/m, no ponto A.