FUVEST 2003

Questão 52606

(FUVEST - 2003 - 2 FASE ) Uma mistura constituída de 45 g de cloreto de sódio e 100 mL de água, contida em um balão e inicialmente a 20 ºC, foi submetida à destilação simples, sob pressão de 700 mm Hg, até que fossem recolhidos 50 mL de destilado. O esquema abaixo representa o conteúdo do balão de destilação, antes do aquecimento:

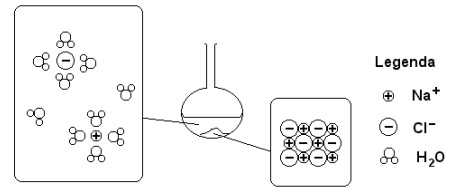
a) De forma análoga à mostrada acima, represente a fase de vapor, durante a ebulição.

b) Qual a massa de cloreto de sódio que está dissolvida, a 20 ºC, após terem sido recolhidos 50 mL de destilado? Justifique.

c) A temperatura de ebulição durante a destilação era igual, maior ou menor que 97,4 ºC? Justifique.

Dados: Curva de solubilidade do cloreto de sódio em água:

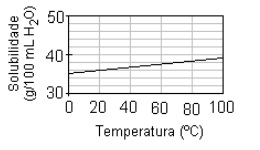
Ponto de ebulição da água pura a 700 mm Hg: 97,4 ºC

Questão 52608

(FUVEST - 2003 - 2 FASE ) Dimetil-hidrazina e tetróxido de dinitrogênio foram usados nos foguetes do módulo que pousou na Lua nas missões Apollo. A reação, que ocorre pela simples mistura desses dois compostos, pode ser representada por (

a) Entre os reagentes, identifique o oxidante e o redutor. Justifique sua resposta, considerando os números de oxidação do carbono e do nitrogênio.

b) Cite duas características da reação apresentada que tornam adequado o uso desses reagentes.

c) Qual a pressão parcial do gás nitrogênio quando a pressão da mistura gasosa liberada se iguala à pressão na superfície da Lua? Mostre os cálculos.

Dados: número de oxidação do carbono na dimetil-hidrazina: -2

pressão na superfície lunar: 3 x   Pa

Questão 52609

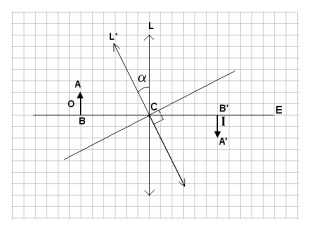
(FUVEST - 2003 - 2 FASE ) A figura na folha de respostas representa, na linguagem da óptica geométrica, uma lente L de eixo E e centro C, um objeto O com extremidades A e B, e sua imagem I com extremidades A’ e B’. Suponha que a lente L seja girada de um ângulo α em torno de um eixo perpendicular ao plano do papel e fique na posição L* indicada na figura. Responda as questões, na figura da folha de respostas, utilizando os procedimentos e as aproximações da óptica geométrica. Faça as construções auxiliares a lápis e apresente o resultado final utilizando caneta.

a) Indique com a letra F as posições dos focos da lente L.

b) Represente, na mesma figura, a nova imagem I* do objeto O, gerada pela lente L*, assinalando os extremos de I* por A* e por B*.

.

Questão 52610

(FUVEST - 2003 - 2 FASE ) Um recipiente cilíndrico contém 1,5 L (litro) de água à temperatura de 40ºC. Uma tampa, colocada sobre a superfície da água, veda o líquido e pode se deslocar verticalmente sem atrito. Um aquecedor elétrico E, de 1800 W, fornece calor à água. O sistema está isolado termicamente de forma que o calor fornecido à água não se transfere ao recipiente. Devido ao peso da tampa e à pressão atmosférica externa, a pressão sobre a superfície da água permanece com o valor P0=1,00×   Pa. Ligando-se o aquecedor, a água esquenta até atingir, depois de um intervalo de tempo tA, a temperatura de ebulição (100ºC). A seguir a água passa a evaporar, preenchendo a região entre a superfície da água e a tampa, até que, depois de mais um intervalo de tempo tB, o aquecedor é desligado. Neste processo, 0,27 mol de água passou ao estado de vapor.

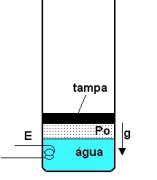
Determine

a) o intervalo de tempo tA, em segundos, necessário para levar a água até a ebulição.

b) o intervalo de tempo tB, em segundos, necessário para evaporar 0,27 mol de água.

c) o trabalho τ, em joules, realizado pelo vapor de água durante o processo de ebulição.

Questão 52611

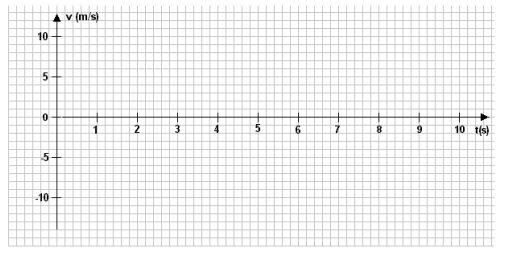
(FUVEST - 2003 - 2 FASE ) Considere uma bolinha, de pequeno raio, abandonada de uma certa altura, no instante t=0, a partir do repouso, acima de uma pesada placa metálica horizontal. A bolinha atinge a placa, pela primeira vez, com velocidade V = 10 m/s, perde parte de sua energia cinética, volta a subir verticalmente e sofre sucessivos choques com a placa. O módulo da velocidade logo após cada choque vale 80% do módulo da velocidade imediatamente antes do choque (coeficiente de restituição = 0,80). A aceleração da gravidade no local é g = 10m/ . Suponha que o movimento ocorra no vácuo.

a) Construa, na figura da folha de respostas, o gráfico da velocidade da bolinha em função do tempo, desde o instante t=0, em que ela é abandonada, até o terceiro choque com a placa. Considere positivas as velocidades com sentido para cima e negativas, as para baixo.

b) Determine o módulo V3 da velocidade da bolinha logo após o terceiro choque.

c) Analisando atentamente o gráfico construído, estime o instante T, a partir do qual a bolinha pode ser considerada em repouso sobre a placa.

Questão 52612

(FUVEST - 2003 - 2 FASE ) Alienígenas desejam observar o nosso planeta. Para tanto, enviam à Terra uma nave N, inicialmente ligada a uma nave auxiliar A, ambas de mesma massa. Quando o conjunto de naves se encontra muito distante da Terra, sua energia cinética e sua energia potencial gravitacional são muito pequenas, de forma que a energia mecânica total do conjunto pode ser considerada nula. Enquanto o conjunto é acelerado pelo campo gravitacional da Terra, sua energia cinética aumenta e sua energia potencial fica cada vez mais negativa, conservando a energia total nula. Quando o conjunto N-A atinge, com velocidade   (a ser determinada), o ponto P de máxima aproximação da Terra, a uma distância  de seu centro, um explosivo é acionado, separando N de A. A nave N passa a percorrer, em torno da Terra, uma órbita circular de raio , com velocidade  (a ser determinada). A nave auxiliar A, adquire uma velocidade   (a ser determinada). Suponha que a Terra esteja isolada no espaço e em repouso.

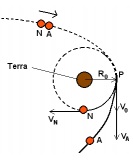
Determine, em função de M, G e ,

a) a velocidade   com que o conjunto atinge o ponto P.

b) a velocidade , de N, em sua órbita circular .

c) a velocidade  de A, logo após se separar de N.

Questão 52613

(FUVEST - 2003 - 2 FASE ) Um avião voa horizontalmente sobre o mar com velocidade V constante (a ser determinada). Um passageiro, sentado próximo ao centro de massa do avião, observa que a superfície do suco de laranja, que está em um copo sobre a bandeja fixa ao seu assento, permanece paralela ao plano da bandeja. Estando junto à janela, e olhando numa direção perpendicular à da trajetória do avião, o passageiro nota que a ponta da asa esquerda do avião tangencia a linha do horizonte, como mostra a figura A. O piloto anuncia que, devido a um problema técnico, o avião fará uma curva de 180º para retornar ao ponto de partida. Durante a curva, o avião se inclina para a esquerda, de um ângulo θ = 30º , sem que haja alterações no módulo de sua velocidade e na sua altura. O passageiro, olhando sempre na direção perpendicular à da velocidade do avião, observa que a ponta da asa esquerda permanece durante toda a curva apontando para um pequeno rochedo que aflora do mar, como representado na figura B. O passageiro também nota que a superfície do suco permaneceu paralela à bandeja, e que o avião percorreu a trajetória semicircular de raio R (a ser determinado), em 90s. Percebe, então, que com suas observações, e alguns conhecimentos de Física que adquiriu no Ensino Médio, pode estimar a altura e a velocidade do avião.

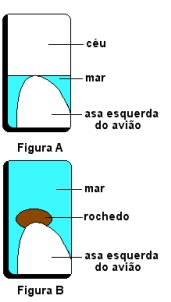
a) Encontre uma relação entre V, R, g e θ , para a situação descrita.

b) Estime o valor da velocidade V do avião, em km/h ou m/s.

c) Estime o valor da altura H, acima do nível do mar, em metros, em que o avião estava voando.

Questão 52614

(FUVEST - 2003 - 2 FASE ) Uma lâmpada L está ligada a uma bateria B por 2 fios, F1 e F2, de mesmo material, de comprimentos iguais e de diâmetros d e 3d, respectivamente. Ligado aos terminais da bateria, há um voltímetro ideal M (com resistência interna muito grande), como mostra a figura. Nestas condições a lâmpada está acesa, tem resistência RL =2,0 Ω e dissipa uma potência igual a 8,0W. A força eletromotriz da bateria é ε = 9,0V e a resistência do fio F1 é R1=1,8 Ω .

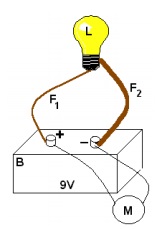
Determine o valor da

a) corrente I , em ampères, que percorre o fio F1.

b) potência P2, em watts, dissipada no fio F2.

c) diferença de potencial VM, em volts, indicada pelo voltímetro M.

Questão 52615

(FUVEST - 2003 - 2 FASE ) A figura representa uma câmara fechada C, de parede cilíndrica de material condutor, ligada à terra. Em uma de suas extremidades, há uma película J, de pequena espessura, que pode ser atravessada por partículas. Coincidente com o eixo da câmara, há um fio condutor F mantido em potencial positivo em relação à terra. O cilindro está preenchido com um gás de tal forma que partículas alfa, que penetram em C, através de J, colidem com moléculas do gás podendo arrancar elétrons das mesmas. Neste processo, são formados íons positivos e igual número de elétrons livres que se dirigem, respectivamente, para C e para F. O número de pares elétron-ion formados é proporcional à energia depositada na câmara pelas partículas alfa, sendo que para cada 30eV de energia perdida por uma partícula alfa, um par é criado. Analise a situação em que um número n = 2x  partículas alfa, cada uma com energia cinética igual a 4,5MeV, penetram em C, a cada segundo, e lá perdem toda a sua energia cinética. Considerando que apenas essas partículas criam os pares elétron-ion, determine :

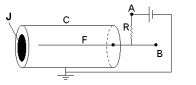
a) o número N de elétrons livres produzidos na câmara C a cada segundo.

b) a diferença de potencial V entre os pontos A e B da figura, sendo a resistência R=5x Ω.

Questão 52616

(FUVEST - 2003 - 2 FASE ) O ímã representado na figura, com largura L = 0,20 m, cria, entre seus pólos, P1 e P2, um campo de indução magnética B, horizontal, de intensidade constante e igual a 1,5T. Entre os pólos do ímã, há um fio condutor f, com massa m=6,0 x  kg, retilíneo e horizontal, em uma direção perpendicular à do campo B. As extremidades do fio, fora da região do ímã, estão apoiadas e podem se mover ao longo de guias condutores, verticais, ligados a um gerador de corrente G. A partir de um certo instante, o fio f passa a ser percorrido por uma corrente elétrica constante I = 50A. Nessas condições, o fio sofre a ação de uma força F0, na direção vertical, que o acelera para cima. O fio percorre uma distância vertical d = 0,12 m, entre os pólos do ímã e, a seguir, se desconecta dos guias, prosseguindo em movimento livre para cima, até atingir uma altura máxima H.

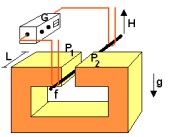
Determine:

a) o valor da força eletromagnética F0, em newtons, que age sobre o fio.

b) o trabalho total τ, em joules, realizado pela força F0.

c) a máxima altura H, em metros, que o fio alcança, medida a partir de sua posição inicial.