FUVEST 2003
Questão 52479
FUVEST
(FUVEST - 2003 - 1a Fase) As soluções da equação
, onde
é diferente de zero, são:
Questão 52482
FUVEST
(FUVEST - 2003 - REDAÇÃO)
Leia atentamente os três textos abaixo.
Texto I
Está no dicionário Houaiss:
auto-estima s.f. qualidade de quem se valoriza, se contenta com seu modo de ser e demonstra, conseqüentemente, confiança em seus atos e julgamentos.
A definição do dicionário parece limitar-se ao âmbito do indivíduo, mas a palavra autoestima já há algum tempo é associada a uma necessidade coletiva. Por exemplo: nós, brasileiros, precisamos fortalecer nossa auto-estima. Neste caso, a satisfação com nosso modo de ser, como povo, nos levaria à confiança em nossos atos e julgamentos. Mas talvez seja o caso de perguntar: não são os nossos atos e julgamentos que acabam por fortalecer ou enfraquecer nossa autoestima, como indivíduos ou como povo?
Texto II
Estão num poema de Drummond, da década de vinte, os versos:
E a gente viajando na pátria sente saudades da pátria.
(...)
Aqui ao menos a gente sabe que é tudo uma canalha só.
Texto III
Está num artigo do jornalista Zuenir Ventura, de dois anos atrás:
De um país em crise e cheio de mazelas, onde, segundo o IBGE, quase um quarto da população ganha R$ 4 por dia, o que se esperaria? Que fosse a morada de um povo infeliz, cético e pessimista, não?
Não. Por incrível que pareça, não. Os brasileiros não só consideram seu país um lugar bom e ótimo para viver, como estão otimistas em relação a seu futuro e acreditam que ele se transformará numa superpotência econômica em cinco anos. Pelo menos essa é a conclusão de um levantamento sobre a “utopia brasileira” realizado pelo Datafolha.
Com o apoio dos três textos apresentados, escreva uma dissertação em prosa, na qual você deverá discutir manifestações concretas de afirmação ou de negação da auto-estima entre os brasileiros. Apresente argumentos que dêem sustentação ao ponto de vista que você adotou.
Ver questãoQuestão 52551
FUVEST
(FUVEST - 2003 - 2 FASE ) a) Quantos múltiplos de 9 há entre 100 e 1000?
b) Quantos múltiplos de 9 ou 15 há entre 100 e 1000?
Ver questãoQuestão 52552
FUVEST
(FUVEST - 2003 - 2 FASE ) Um caminhão transporta maçãs, pêras e laranjas, num total de 10.000 frutas. As frutas estão condicionadas em caixas (cada caixa só contém um tipo de fruta), sendo que cada caixa de maçãs, pêras e laranjas, tem, respectivamente 50 maçãs, 60 pêras e 100 laranjas e custam, respectivamente, 20, 40 e 10 reais. Se a carga do caminhão tem 140 caixas e custa 3300 reais, calcule quantas maçãs, pêras e laranjas estão sendo transportadas.
Ver questãoQuestão 52553
FUVEST
(FUVEST - 2003 - 2 FASE ) a) A reta r passa pela origem do plano cartesiano e tem coeficiente angular m > 0 . A circunferência C passa pelos pontos (1, 0 ) e (3,0) e tem centro no eixo x. Para qual valor de m a reta r é tangente a C?
b) Suponha agora que o valor de m seja menor que aquele determinado no item anterior. Calcule a área do triângulo determinado pelo centro de C e pelos pontos de intersecção de r com C.
Ver questãoQuestão 52554
FUVEST
(FUVEST - 2003 - 2 FASE ) Em uma equipe de basquete, a distribuição de idades dos seus jogadores é a seguinte:
| IDADE | Nº DE JOGADORES |
| 22 | 1 |
| 25 | 3 |
| 26 | 4 |
| 29 | 1 |
| 31 | 2 |
| 32 | 1 |
Será sorteada, aleatoriamente, uma comissão de dois jogadores que representará a equipe junto aos dirigentes.
a) Quantas possibilidades distintas existem para formar esta comissão?
b) Qual a probabilidade da média de idade dos dois jogadores da comissão sorteada ser estritamente menor que a média de idade de todos os jogadores?
Ver questãoQuestão 52555
FUVEST
(FUVEST - 2003 - 2 FASE ) Na figura ao abaixo, M é o ponto médio da corda PQ da circunferência e PQ = 8 . O segmento RM é perpendicular a PQ e RM = . Calcule:
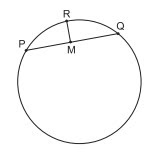
a) O raio da circunferência.
b) A medida do ângulo , onde O é o centro da circunferência.
Questão 52556
FUVEST
(FUVEST - 2003 - 2 FASE ) Na figura abaixo , as circunferências têm centros A e B. O raio da maior é do raio da menor; P é um ponto de intersecção delas e a reta AQ é tangente à circunferência menor no ponto Q. Calcule:
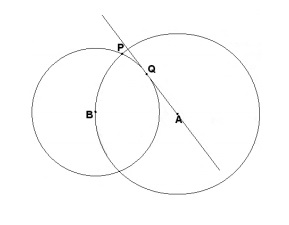
a) cos .
b) cos .
c) cos .
Questão 52557
FUVEST
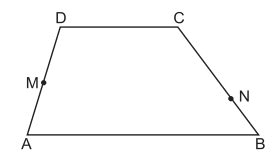
(FUVEST - 2003 - 2 FASE ) No trapézio ABCD, M é o ponto médio do lado AD ; N está sobre o lado BC e 2BN = NC . Sabe-se que as áreas dos quadriláteros ABNM e CDMN são iguais e que DC = 10 . Calcule AB.
 .
.
Questão 52558
FUVEST
(FUVEST - 2003 - 2 FASE ) Nos itens abaixo, z denota um número complexo e i a unidade imaginária ( ). Suponha z ≠ i .
a) Para quais valores de z tem-se ?
b) Determine o conjunto de todos os valores de z para os quais é um número real.