FUVEST 2007

Questão 50915

(UNICAMP - 2007) Em muitas praças de pedágio de rodovias existe um sistema que permite a abertura automática da cancela. Ao se aproximar, um veículo munido de um dispositivo apropriado é capaz de trocar sinais eletromagnéticos com outro dispositivo na cancela. Ao receber os sinais, a cancela abre-se automaticamente e o veículo é identificado para posterior cobrança. Para as perguntas a seguir, desconsidere o tamanho do veículo.

a) Um veículo aproxima-se da praça de pedágio a 40 km/h. A cancela recebe os sinais quando o veículo se encontra a 50 m de distância. Qual é o tempo disponível para a completa abertura da cancela?
b) O motorista percebe que a cancela não abriu e aciona os freios exatamente quando o veículo se encontra a 40 m da mesma, imprimindo uma desaceleração de módulo constante. Qual deve ser o valor dessa desaceleração para que o veículo pare exatamente na cancela?

Questão 50916

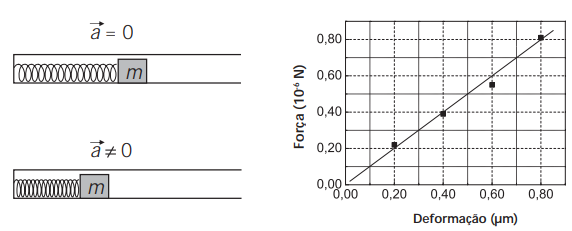
(UNICAMP - 2007) Sensores de dimensões muito pequenas têm sido acoplados a circuitos micro-eletrônicos. Um exemplo é um medidor de aceleração que consiste de uma massa m presa a uma micro-mola de constante elástica k. Quando o conjunto é submetido a uma aceleração , a micro-mola se deforma, aplicando uma força na massa (ver diagrama abaixo). O gráfico ao lado do diagrama mostra o módulo da força aplicada versus a deformação de uma micro-mola utilizada num medidor de aceleração.

a) Qual é a constante elástica k da micro-mola?

b) Qual é a energia necessária para produzir uma compressão de na micro-mola?

c) O medidor de aceleração foi dimensionado de forma que essa micro-mola sofra uma deformação de quando a massa tem uma aceleração de módulo igual a 25 vezes o da aceleração da gravidade. Qual é o valor da massa m ligada à micro-mola?

Questão 50917

(UNICAMP - 2ª FASE - 2007) Suponha que o esquilo do filme “A Era do Gelo” tenha desenvolvido uma técnica para recolher nozes durante o percurso para sua toca. Ele desliza por uma rampa até atingir uma superfície plana com velocidade de 10 m/s. Uma vez nessa superfície, o esquilo passa a apanhar nozes em seu percurso. Todo o movimento se dá sobre o gelo, de forma que o atrito pode ser desprezado. A massa do esquilo é de 600 g e a massa de uma noz é de 40 g.
a) Qual é a velocidade do esquilo após colher 5 nozes?
b) Calcule a variação da energia cinética do conjunto formado pelo esquilo e pelas nozes entre o início e o final da coleta das 5 nozes.

Questão 50918

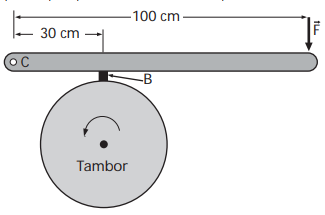
(UNICAMP - 2ª FASE - 2007) Um freio a tambor funciona de acordo com o esquema da figura abaixo. A peça de borracha B é pressionada por uma alavanca sobre um tambor cilíndrico que gira junto com a roda. A alavanca é acionada pela força F e o pino no ponto C é fixo. O coeficiente de atrito cinético entre a peça de borracha e o tambor é µ_c  = 0,40.

a) Qual é o módulo da força normal que a borracha B exerce sobre o tambor quando F = 750 N? Despreze a massa da alavanca.
b) Qual é o módulo da força de atrito entre a borracha e o tambor?
c) Qual é o módulo da força aplicada pelo pino sobre a alavanca no ponto C?

Questão 50919

(UNICAMP - 2ª FASE - 2007)  Uma torneira é usada para controlar a vazão  da água que sai de um determinado encanamento. Essa vazão (volume de água por unidade de
tempo) relaciona-se com a diferença de pressão dos dois lados da torneira (ver figura) pela seguinte expressão:

Nesta expressão, Z é a resistência ao fluxo de água oferecida pela torneira. A densidade da água é 1,0 x 10³  kg/m³  e a pressão atmosférica P₀  é igual a 1,0 × 10⁵  N/m².

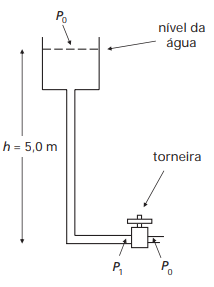
a) Qual é a unidade de Z no Sistema Internacional?
b) Se a torneira estiver fechada, qual será a pressão P₁?
c) Faça uma estimativa da vazão de uma torneira doméstica, tomando como base sua experiência cotidiana. A partir dessa estimativa, encontre a resistência da torneira, supondo que a diferença de pressão (P₁ – P₀) seja igual a 4,0 × 10⁴  N/m².

Questão 50920

(UNICAMP - 2ª FASE - 2007)  Em agosto de 2006, Plutão foi reclassificado pela União Astronômica Internacional, passando a ser considerado um planeta-anão. A terceira Lei de Kepler diz que onde T é o tempo para um planeta completar uma volta em torno do Sol, e a é a média entre a maior e a menor distância do planeta ao Sol. No caso da Terra, essa média é a_T  = 1,5 x 10¹¹ m, enquanto que para Plutão a_P  = 60 x 10¹¹ m. A constante K é a mesma para todos os objetos em órbita em torno do Sol. A velocidade da luz no vácuo é igual a 3,0 x 10⁸  m/s. Dado: .

a) Considerando-se as distâncias médias, quanto tempo leva a luz do Sol para atingir a Terra? E para atingir Plutão?
b) Quantos anos terrestres Plutão leva para dar uma volta em torno do Sol? Expresse o resultado de forma aproximada como um número inteiro.

Questão 50921

(UNICAMP - 2ª FASE - 2007) O nível sonoro S é medido em decibéis (dB) de acordo com a expressão onde I é a intensidade da onda sonora e I0  = 10-12 W/m² é a intensidade de referência padrão correspondente ao limiar da audição do ouvido humano. Numa certa construção, o uso de proteção auditiva é indicado para trabalhadores expostos durante um dia de trabalho a um nível igual ou superior a 85 dB. O gráfico abaixo mostra o nível sonoro em função da distância a uma britadeira em funcionamento na obra. 

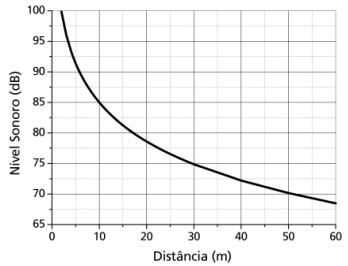
a) A que distância mínima da britadeira os trabalhadores podem permanecer sem proteção auditiva?
b) A frequência predominante do som emitido pela britadeira é de 100 Hz. Sabendo-se que a velocidade do som no ar é de 340 m/s, qual é o comprimento de onda para essa frequência?
c) Qual é a intensidade da onda sonora emitida pela britadeira a uma distância de 50 m? 

Questão 50922

(UNICAMP - 2ª FASE - 2007)  Nas regiões mais frias do planeta, camadas de gelo podem se formar rapidamente sobre um volume de água a céu aberto. A figura abaixo mostra um tanque cilíndrico de água cuja área da base é A = 2,0 m², havendo uma camada de gelo de espessura L na superfície da água. O ar em contato com o gelo está a uma temperatura T_ar = –10 ºC, enquanto a temperatura da água em contato com o gelo é T_ag = 0,0 ºC

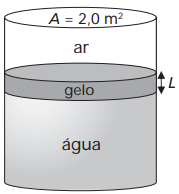
a) O calor é conduzido da água ao ar através do gelo. O fluxo de calor , definido como a quantidade de calor conduzido por unidade de tempo, é dado por , onde k = 4,0 x 10^-3 cal/(s cm ºC) é a condutividade térmica do gelo. Qual é o fluxo de calor  quando L = 5,0 cm?
b) Ao solidificar-se, a água a 0 ºC perde uma quantidade de calor que é proporcional à massa de água transformada em gelo. A constante de proporcionalidade L_S é chamada de calor latente de solidificação. Sabendo-se que o calor latente de solidificação e a densidade do gelo valem, respectivamente, L_S  = 80 cal/g e g  = 0,90 g/cm³, calcule a quantidade de calor trocado entre a água e o ar para que a espessura do gelo aumente de 5,0 cm para 15 cm.

Questão 50923

(UNICAMP - 2ª FASE - 2007) O diagrama abaixo representa um circuito simplificado de uma torradeira elétrica que funciona com uma tensão U = 120 V. Um conjunto de resistores R_T = 20 Ω é responsável pelo aquecimento das torradas e um cronômetro determina o tempo durante o qual a torradeira permanece ligada.

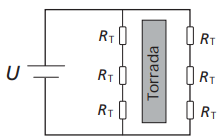
a) Qual é a corrente que circula em cada resistor R_T quando a torradeira está em funcionamento?
b) Sabendo-se que essa torradeira leva 50 segundos para preparar uma torrada, qual é a energia elétrica total consumida no preparo dessa torrada?
c) O preparo da torrada só depende da energia elétrica total dissipada nos resistores. Se a torradeira funcionasse com dois resistores R_T de cada lado da torrada, qual seria o novo tempo de preparo da torrada?

Questão 50924

(UNICAMP - 2ª FASE - 2007)  Numa tela de televisor de plasma, pequenas células contendo uma mistura de gases emitem luz quando submetidas a descargas elétricas. A figura abaixo mostra uma célula com dois eletrodos, nos quais uma diferença de potencial é aplicada para produzir a descarga. Considere que os eletrodos formam um capacitor de placas paralelas, cuja capacitância é dada por , onde , A é a área de cada eletrodo e d é a distância entre os eletrodos.

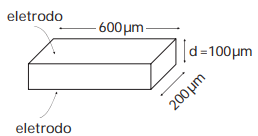
a) Calcule a capacitância da célula.
b) A carga armazenada em um capacitor é proporcional à diferença de potencial aplicada, sendo que a constante de proporcionalidade é a capacitância. Se uma diferença de potencial igual a 100 V for aplicada nos eletrodos da célula, qual é a carga que será armazenada?
c) Se a carga encontrada no item b) atravessar o gás em (tempo de descarga), qual será a corrente média?