ITA 2024

Questão 81911

(ITA - 2024)

Com base em seus conhecimentos e em pelo menos um dos itens da coletânea, escreva uma dissertação a respeito da responsabilidade da engenharia frente aos problemas do mundo contemporâneo. Dê um título ao texto.

Item 1.

A primeira explosão de uma bomba nuclear aconteceu em 16 de junho de 1945, em um local conhecido como “jornada del muerto”, no estado do Novo México, EUA. Chamada pelo nome codificado de “Trinity test”, essa explosão confirmou que uma bomba atômica de plutônio poderia ser prontamente utilizada pelas forças armadas dos EUA. Vinte anos mais tarde, em 1965, o físico J. Robert Oppenheimer, um dos líderes do projeto Manhattan, fez uma declaração em que parafraseia o capítulo 11, verso 32, do Bhagavad Gita: “Eu sou o tempo, o grande destruidor de mundos”. Suas palavras foram:

“Sabíamos que o mundo não seria o mesmo. Algumas pessoas riram, umas poucas choraram. A maioria ficou em silêncio. Lembrei-me da frase da escritura hindu, o Bhagavad Gita. Vishnu está tentando persuadir o príncipe de que ele deve cumprir seu dever e, para impressioná-lo, assume a sua forma de muitos braços e diz: ‘Agora tornei-me a Morte, a destruidora de mundos’. Acho que todos nós [naquele momento] pensamos isso, de uma forma ou de outra.”

[Disponível em: . Acesso em: 20 ago. 2023. Trad. ITA].

Item 2.

Em 1918, Santos Dumont escreve sobre os seus sentimentos ao receber de Albert R. Hawley, presidente do Aero Club da América, EUA, uma carta com o relato do estabelecimento da primeira linha de correio aéreo naquele país:

“Esta carta veio encher de legítima alegria o meu coração que, há já quatro anos, sofre com as notícias da mortandade terrível causada, na Europa, pela aeronáutica. Nós, os fundadores da locomoção aérea no fim do século passado, tínhamos sonhado um futuroso caminho de glória pacífica para essa filha dos nossos desvelos. Lembro-me perfeitamente que, naquele fim de século e nos primeiros anos do atual, no Aero Club de França, que foi, pode-se dizer, ‘O ninho da aeronáutica’ e que era o ponto de reunião de todos os inventores que se ocupavam dessa ciência, pouco se falou em guerra; prevíamos que os aeronautas poderiam, talvez, no futuro, servir de esclarecedores para os Estados-maiores dos exércitos, nunca, porém, veio-nos a ideia de que eles pudessem desempenhar funções destruidoras nos combates. Bastante conheci todos esses sonhadores, centenas dos quais deram a vida pela nossa ideia, para poder agora afirmar que jamais nos passou pela mente que pudessem, no futuro, os nossos sucessores ser ‘mandados’ a atacar cidades indefesas, cheias de crianças, mulheres e velhos e, o que é mais, atacar hospitais onde a abnegação e o humanitarismo dos rivais reúnem, sob o mesmo teto e o mesmo carinho, os feridos e moribundos dos dois campos.”

[Santos-Dumont. O que eu vi, o que nós veremos, 1918, pp. 6-7. Domínio público].

Questão 81912

(ITA - 2024)

Considere um banco de três pernas, todas de mesmo comprimento, com um assento em formato de disco de raio R e massa m. Este banco está sobre uma superfície horizontal perfeitamente plana e os seus pés tocam o solo em três pontos que correspondem aos vértices de um triângulo equilátero de aresta l. O banco é construído de tal forma que o eixo de simetria do assento intercepta o centro geométrico do triângulo. Uma barra de massa Me comprimento L > 2R é afixada sobre o banco, de modo que uma de suas extremidades permanece junto à borda do assento e a outra ultrapassa os seus limites. A barra passa pelo centro do assento e está orientada na mesma direção que uma das mediatrizes do triângulo equilátero. A figura mostra o banco, com a barra, em vista superior.

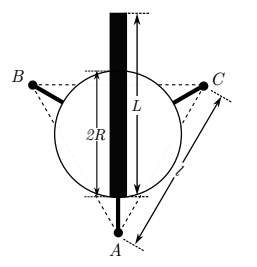
Considerando este sistema, responda aos seguintes itens: 

a) supondo que o sistema está em condição de equilíbrio, determine a expressão da reação normal do piso sobre o pé do banco que está apoiado no ponto A;

b) determine o intervalo de valores de L para os quais o banco permanece em equilíbrio, mantidos todos os outros parâmetros fixos.

Questão 81913

(ITA - 2024)

Um professor desenvolveu um projeto para o estudo de ondas estacionárias em cordas. Para tal, utilizou um gerador de frequência f, um fio de náilon de densidade linear de massa , dois pedestais universais, uma roldana e um bloco de massa m. A distância da roldana até o gerador é l₀. Toda a montagem foi acoplada sobre uma plataforma de madeira com rodas permitindo sua locomoção ao longo do eixo x, con- forme mostra a figura. A massa total do sistema era M. Em repouso, o gerador de frequências foi ajustado para que a vibração na corda apresentasse uma única crista.

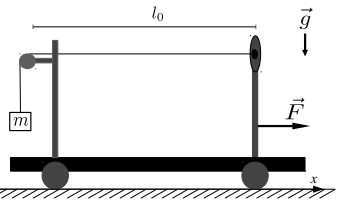
Uma vez que a frequência de ajuste no gerador seja dobrada com relação à frequência inicial, qual deve ser a força F aplicada sobre o sistema para que se visualize uma única crista novamente? Despreze o atrito.

Questão 81914

(ITA - 2024)

Considere duas situações: (i) uma partícula A de massa m e carga q, sob influência de uma campo elétrico constante é colocada para oscilar pela ação de uma mola de rigidez k e comprimento livre l₀, ao longo do eixo x; (ii) uma segunda partícula, B, é conectada à A, pela mesma mola, na presença de . A partícula B é neutra e tem massa m.

Desconsiderando efeitos de radiação eletromagnética e de atrito, determine:

a) o período de oscilação do sistema massa-mola na situação (i);

b) a frequência angular  de oscilação da massa A em relação ao centro de massa na situação (ii);

c) a equação horária de cada partícula em (ii), sabendo que, inicialmente, a massa A está em repouso e passa pela origem do sistema de coordenadas, ao passo que a massa B também está em repouso e se encontra a uma distância l₀ de A.

Questão 81915

(ITA - 2024)

Um grupo de estudantes estava trabalhando na concepção de termômetro a gás a volume constante, conforme a figura. Com intuito de calibrar o termômetro, os estudantes mediram a pressão do gás, P₀, a 0°C. Em seguida, o bulbo de vidro do termômetro foi posto em contato com uma quantidade de água a 100°C, resultando em uma elevação h da coluna de mercúrio, constituindo assim uma escala de temperatura. Entretanto, notou-se que a altura h, atingida pelo mercúrio, não correspondia, de forma precisa, aos valores calculados inicialmente. Após muitas discussões os estudantes concluíram que a expansão térmica do bulbo foi a causa dessa discrepância.

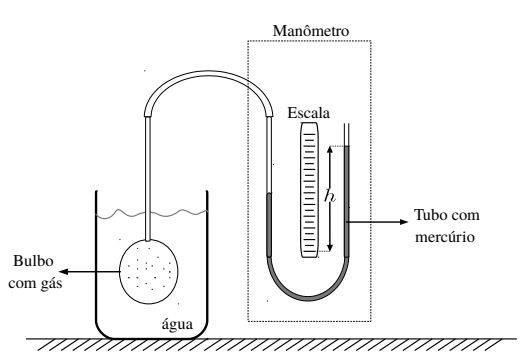
Dado o exposto e assumindo que a densidade do mercúrio seja dada por  a aceleração gravitacional por g, responda aos itens abaixo.

a) Assumindo que o gás no interior do bulbo seja ideal, calcule o valor relativo à altura h desconsiderando o efeito de dilatação térmica do bulbo.

b) Sabendo que V₀ é o volume do bulbo à 0°C e que a é o coeficiente de dilatação linear do vidro, calcule qual deve ser a diferença entre o valor medido de h e o valor calculado inicialmente se esta fosse a única causa da discrepância. Despreze as dimensões do orifício de contato entre o bulbo e o capilar.

Questão 81916

(ITA - 2024)

Considere dois objetos idênticos inicialmente em equilíbrio térmico à temperatura T₁. Um refrigerador realiza trabalho W e faz um dos objetos atingir a temperatura T₂. Considere que os objetos não trocam calor com o meio externo e tudo acontece a pressão constante. Sendo C_p a capacidade térmica de cada objeto a pressão constante, qual o valor mínimo de W?

Dado: A variação de entropia  a pressão constante entre temperaturas  e  é  

Questão 81917

(ITA - 2024)

Um observatório analisa a frequência de uma emissão eletromagnética, de frequência natural f_e, proveniente de duas estrelas que formam um sistema binário com órbitas circulares. O gráfico obtido está representado na figura.

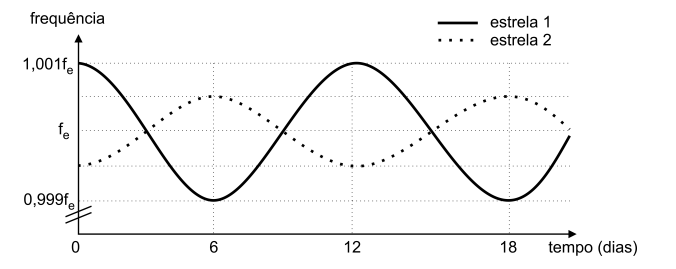
Com base nesse gráfico, estime:

a) a distância que separa as duas estrelas em metros;

b) a massa de cada uma das estrelas em quilogramas.

Questão 82385

(ITA - 2024)

Deseja-se focalizar um feixe monocromático paralelo em torno de um ponto F. Devido ao baixo comprimento de onda λ e efeitos de absorção no material, não é possível utilizar uma lente convergente usual para focalizar essa radiação. Como alternativa, utiliza-se uma rede de difração constituída por um arranjo de anéis concêntricos em torno de um círculo absorvedor de raio r₁. Os anéis concêntricos intercalam regiões com obstáculos absorvedores (preto) e sem obstáculos absorvedores (cinza), como indicado na figura.

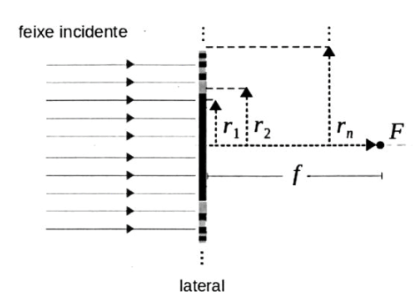
Obtenha uma expressão para os raios r_n(n > 1) dos anéis concêntricos, que podem ser absorvedores (n ímpar) ou sem obstáculos (n par), em função de λ, r₁, da distância f do centro dos anéis ao ponto F e do índice inteiro n, de forma que o arranjo funcione como um focalizador.

Questão 82386

(ITA - 2024)

Quatro cargas idênticas de valor q₁ estão dispostas nos vértices de um quadrado de lado 2a e quatro cargas q₂ estão posicionadas nos pontos médios das arestas, conforme mostra a figura.

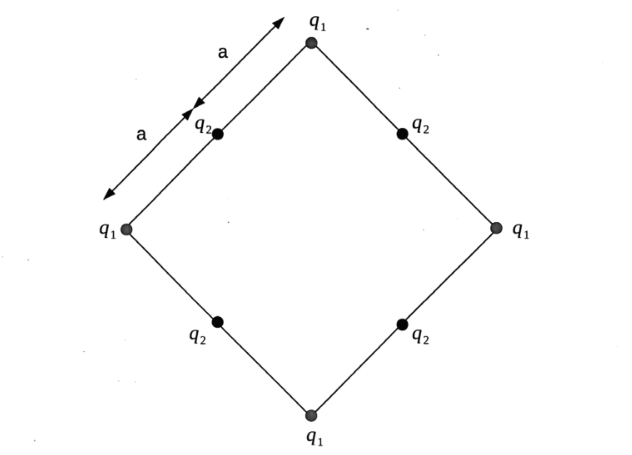
Considerando que o sistema esteja no vácuo, faça o que se pede nos itens a seguir.

a) Obtenha a energia potencial deste sistema de cargas em termos da permissividade elétrica no vácuo є₀, q₁, q₂ e a.

b) Sabendo que as cargas q₂ estão fixas, determine qual deve ser a razão q₁/q₂ para que o sistema permaneça em equilíbrio estático.

Questão 82387

(ITA - 2024)

Um painel solar é um gerador elétrico capaz de converter energia luminosa em energia elétrica. Uma vez exposto à luz solar, processos físicos geram uma diferença de potencial elétrico capaz de gerar corrente elétrica. Uma curva característica I – V de um dispositivo como esse é fornecida abaixo.

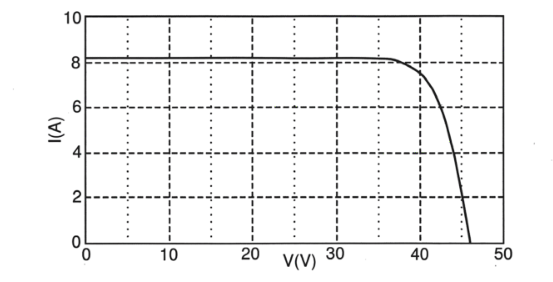
Faça o que se pede nos itens a seguir.

a) Obtenha a força eletromotriz do painel solar.

b) Determine a corrente elétrica gerada pela célula solar quando seus terminais são ligados por resistências de 2,5Ω, 5Ω e 10Ω, respectivamente. Descreva o procedimento usado para chegar à resposta.

c) Faça um esboço do gráfico da potência elétrica P fornecida pela célula solar em função da tensão V entre os terminais do gerador. Indique os pontos de potência nula e se há algum ponto de operação de potência máxima.