FUVEST 2011

Questão 47404

(FUVEST 2011 - 2 fase) Viver numa grande cidade implica o reconhecimento de múltiplos sinais. Trata-se de uma atividade do olhar, de uma identificação visual, de um saber adquirido, portanto. Se o olhar do transeunte, que fixa fortuitamente uma mulher bonita e viúva ou um grupo de moças voltando do trabalho, pressupõe um conhecimento da cor do luto e das vestimentas operárias, também o olhar do assaltante ou o do policial, buscando ambos a sua presa, implica um conhecimento específico da cidade.

Maria Stella Bresciani, Londres e Paris no século XIX: o espetáculo da pobreza. São Paulo: Brasiliense, 1982, p.16. Adaptado.

O texto mostra como o forte crescimento territorial e demográfico de algumas cidades europeias, no século XIX, redefiniu formas de convivência e sociabilidade de seus habitantes as quais, em alguns casos, persistem até hoje.

a) Cite e explique dois motivos do crescimento de cidades como Londres e Paris, no século XIX.

b) Indique e analise uma característica, dentre as mencionadas no texto, que se faça presente em grandes cidades atuais.

Questão 47405

(FUVEST 2011 - 2 fase)

a) Correlacione as informações contidas nos mapas acima.

b) Identifique e explique dois fatores responsáveis por mudanças no padrão espacial de distribuição da população brasileira, ocorridas entre 1991 e 2000.

Questão 47407

(FUVEST 2011 - 2 fase) O processo de formação de cidades brasileiras esteve associado, entre outras situações, à existência de aldeamento indígena, estação de saúde, arraial de mineração, capela, forte, assentamento de imigrantes, rota de tropeiros ou, ainda, à construção de cidades planejadas.

Com base no mapa e em seus conhecimentos:

a) Preencha, no quadro presente na folha de respostas, a legenda correta para o mapa acima.

b) Identifique e explique duas razões para a construção de Brasília, capital do país, que é uma cidade planejada.

Questão 47408

(FUVEST 2011 - 2 fase) Os ventos alísios fazem parte da circulação atmosférica global, soprando das zonas tropicais, de alta pressão, para a zona equatorial, de baixa pressão, sendo responsáveis, por exemplo, pelo transporte de umidade oceânica para o nordeste brasileiro. Esse tipo de vento aparece no poema de João Cabral de Melo Neto “A escola das facas”, publicado em 1980 no livro de mesmo nome, a seguir.

O alísio ao chegar ao Nordeste
baixa em coqueirais, canaviais;
cursando as folhas laminadas,
se afia em peixeiras, punhais.

Por isso, sobrevoada a Mata,
suas mãos, antes fêmeas, redondas,
ganham a fome e o dente da faca
com que sobrevoa outras zonas.

O coqueiro e a cana lhe ensinam,
sem pedra-mó, mas faca a faca
como voar o Agreste e o Sertão:
mão cortante e desembainhada.

a) Existe relação entre o que ocorre com o “alísio”, ao chegar ao Nordeste, e a palavra “escola”, presente no título do poema de João Cabral de Melo Neto? Explique.

b) A umidade do ar, trazida pelos ventos alísios, diminui ao entrar no continente. Descreva e explique duas adaptações evolutivas, relacionadas a esse fato, que diferenciam a vegetação da Zona da Mata da vegetação do Sertão.

Questão 47425

(FUVEST - 2011 - 2ª fase) 

Define-se geometricamente a razão áurea do seguinte modo: O ponto C da figura abaixo divide o segmento AB na razão áurea quando os valores AC/AB e CB/AC são iguais. Esse valor comum é chamado “razão áurea”.

A razão áurea, também denominada proporção áurea, número de ouro ou divina proporção, conquistou a imaginação popular e é tema de vários livros e artigos. Em geral, suas propriedades matemáticas estão corretamente enunciadas, mas muitas afirmações feitas sobre ela na arte, na arquitetura, na literatura e na estética são falsas ou equivocadas. Infelizmente, essas afirmações sobre a razão áurea foram amplamente divulgadas e adquiriram status de senso comum. Mesmo livros de geometria utilizados no ensino médio trazem conceitos incorretos sobre ela.

Trecho traduzido e adaptado do artigo de G. Markowsky, Misconceptions about the golden ratio, The College Mathematics Journal, 23, 1, january, 1992, pp. 2-19.

a) Reescreva o trecho “(...) mas muitas afirmações feitas sobre ela na arte, na arquitetura, na literatura e na estética são falsas ou equivocadas”, substituindo a conjunção que o inicia por “embora”, com as devidas alterações.

b) O verbo da oração “Infelizmente, essas afirmações sobre a razão áurea foram amplamente divulgadas” está na voz passiva analítica. Reescreva-a com o verbo na voz passiva sintética, fazendo as devidas alterações.

c) Na figura presente no espaço destinado à resposta desta questão, o polígono ADEFG é um pentágono regular. Utilize semelhança de triângulos para demonstrar que o ponto C da figura divide o segmento AB na razão áurea.

Questão 47426

(FUVEST - 2011 - 2 fase)

a) Sendo ݅ a unidade imaginária, determine as partes real e imaginária do número complexo

b) Determine um polinômio de grau 2, com coeficientes inteiros, que tenha z₀ como raiz.

c) Determine os números complexos w tais que z₀.w  tenha módulo igual a  e tais que as partes real e imaginária de z₀.w sejam iguais.

d) No plano complexo, determine o número complexo z₁  que é o simétrico de z₀ com relação à reta de equação y-x=0.

Questão 47427

(FUVEST - 2011 - 2 fase)

A borracha natural apresenta propriedades que limitam o seu uso. Por exemplo, ao ser aquecida, torna-se mole e pegajosa. O processo de vulcanização da borracha, desenvolvido a partir de 1839 e exemplificado na figura abaixo, permitiu a produção de pneus, mangueiras e outros utensílios incorporados à vida cotidiana. A utilidade industrial da borracha estimulou sua exploração comercial a partir das seringueiras da Amazônia. A produção brasileira desse produto dominou o mercado mundial até 1913, quando foi superada pela produção proveniente do cultivo de seringueiras na Ásia.

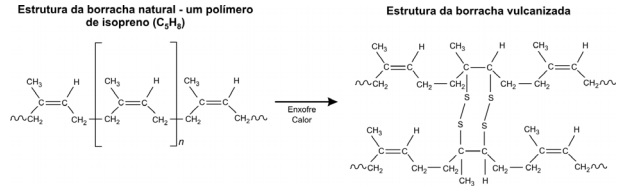
a) Por que a adição de enxofre, no processo de vulcanização, altera as características mecânicas da borracha natural?

b) Supondo que 16 g de enxofre foram adicionados a 1000 g de borracha natural pelo processo de vulcanização, exemplificado no esquema acima, responda: Que porcentagem de unidades de isopreno foi modificada por ligações cruzadas? (Massas molares: H = 1 g/mol, C = 12 g/mol e S = 32 g/mol)

c) Cite e explique uma consequência social provocada pela exploração da borracha na Amazônia até 1913.

Questão 47428

(FUVEST - 2011 - 2 fase)

As circunferências C₁ e C₂ estão centradas em O₁ e O₂, têm raios r₁=3 e r₂=12, respectivamente, e tangenciam-se externamente. Uma reta t é tangente a  C₁  no ponto P₁, tangente a C₂ no ponto P₂ e intercepta a reta O₁O₂ no ponto Q. Sendo assim, determine

a) o comprimento P₁P₂;

b) a área do quadrilátero O₁O₂P₂P₁;

c) a área do triângulo QO₂P_2.

Questão 47429

(FUVEST - 2011 - 2 fase) 

As sensações provocadas nos passageiros, dentro de um carrinho, durante o trajeto em uma montanha-russa, podem ser associadas a determinadas transformações históricas, como se observa no texto:

A primeira é a da ascensão contínua, metódica e persistente. Essa fase pode representar o período que vai, mais ou menos, do século XVI até meados do século XIX. A segunda é a fase em que, num repente, nos precipitamos numa queda vertiginosa, perdendo as referências do espaço, das circunstâncias que nos cercam e até o controle das faculdades conscientes. Isso aconteceu por volta de 1870. Nunca é demais lembrar que esse foi o momento no qual surgiram os parques de diversões e sua mais espetacular atração, a montanha-russa, é claro. A terceira fase, na nossa imagem da montanha-russa, é a do “loop”, a síncope final e definitiva, o clímax da aceleração precipitada. A escala das mudanças desencadeadas, a partir desse momento, é de uma tal magnitude que faz os dois momentos anteriores parecerem projeções em câmara lenta.

N. Sevcenko, No loop da montanha-russa, 2009. Adaptado.

a) Explique duas das fases históricas mencionadas no texto.

b) Na montanha-russa esquematizada abaixo, um motor leva o carrinho até o ponto 1. Desse ponto, ele parte, saindo do repouso, em direção ao ponto 2, localizado em um trecho retilíneo, para percorrer o resto do trajeto sob a ação da gravidade (g = 10 m/s² ).

Desprezando a resistência do ar e as forças de atrito, calcule

1. o módulo da aceleração tangencial do carrinho no ponto 2.

2. a velocidade escalar do carrinho no ponto 3, dentro do loop

Questão 47431

(FUVEST - 2011 - 2 fase)

Os modelos permitem-nos fazer previsões sobre situações reais, sendo, em geral, simplificações, válidas em certas condições, de questões complexas. Por exemplo, num jogo de futebol, a trajetória da bola, após o chute, e o débito cardíaco dos jogadores podem ser descritos por modelos.

• Trajetória da bola: quando se despreza a resistência do ar, a trajetória da bola chutada, sob a ação da gravidade (g=10 m/s²), é dada por  em que v₀ é a velocidade escalar inicial (em m/s),  é o ângulo de elevação (em radianos) e h é a altura (em m) da bola a uma distância d (em m), do local do chute, conforme figura abaixo.

• Débito cardíaco (DC): está relacionado ao volume sistólico VS (volume de sangue bombeado a cada batimento) e à frequência cardíaca FC pela fórmula DC = VS x FC.

Utilize esses modelos para responder às seguintes questões:

a) Durante uma partida, um jogador de futebol quer fazer um passe para um companheiro a 32 m de distância. Seu chute produz uma velocidade inicial na bola de 72 km/h. Calcule os valores de  necessários para que o passe caia exatamente nos pés do companheiro.

b) Dois jogadores, A e B, correndo moderadamente pelo campo, têm frequência cardíaca de 120 batimentos por minuto. O jogador A tem o volume sistólico igual a 4/5 do volume sistólico do jogador B. Os dois passam a correr mais rapidamente. A frequência cardíaca do jogador B eleva-se para 150 batimentos por minuto. Para quanto subirá a frequência cardíaca do jogador A se a variação no débito cardíaco (DC_final-DC_inicial) de ambos for a mesma?