FUVEST 2024
Questão 82482
FUVEST
(FUVEST - 2024)
Leia os excertos para responder à questão.
I.
Quincas Borba
Os personagens de Machado de Assis eram tão medíocres que, enquanto outros loucos do mundo bancavam Napoleão o Grande, o de Machado de Assis contentava-se em ser Napoleão III.
Mario Quintana. Caderno H.
II.
Hegel observa em uma de suas obras que todos os fatos e personagens de grande importância na história do mundo ocorrem, por assim dizer, duas vezes. E esqueceu-se de acrescentar: a primeira vez como tragédia, a segunda como farsa. (...) Os homens fazem sua própria história, mas não a fazem como querem; não a fazem sob circunstâncias de sua escolha e sim sob aquelas com que se defrontam diretamente, legadas e transmitidas pelo passado. A tradição de todas as gerações mortas oprime como um pesadelo o cérebro dos vivos.
Karl Marx. O 18 Brumário de Luís Bonaparte.
a) A mediocridade caracteriza, em geral, o sujeito médio, incapaz de se sobrepor às circunstâncias com que se defronta diretamente. Nesse sentido, Rubião é uma personagem medíocre. Comente.
b) Ao comparar os impérios de tio e sobrinho – Napoleão I e Napoleão III –, na França, Marx considera que os dois golpes representaram, respectivamente, uma tragédia e uma farsa. Por que se pode dizer que a loucura do vencido Rubião, vivida na história brasileira, possui aspectos sérios e risíveis? Justifique.
Ver questãoQuestão 82483
FUVEST
(FUVEST - 2024)
Ao tratar do drama da personagem de Tomás Antonio Gonzaga, o narrador de O romanceiro da Inconfidência descreve-o do seguinte modo:
| “Tanto impou de namorado! | |
| E agora, quando se mira | |
| vê-se um mísero coitado... | |
| (como lá diz numa lira...) | |
| - Se nas águas se mirasse, | |
| veria ralo o cabelo | |
| - Um par de esporas, somente. | |
| E murcha e pálida, a face. | |
| - Falta-lhe aquele desvelo | |
| da sua pastora terna... | |
| - Deveria socorrê-lo.. | |
| -... a quem dará glória eterna!... – | |
| Ai, que ricos libertinos! | |
| Tudo era Inglaterra e França, | |
| e, em redor, versos latinos... | |
| - lá se lhes foi a esperança! | |
| - Mas segue com seus embargos. | |
| (Quem porfia, sempre alcança...) | |
| - Os argumentos são largos. | |
| - Que tem luzes, ninguém nega, | |
| - Mas são coisas da Fortuna, | |
| que bem se sabe ser cega... | |
| - Não lhe sendo a hora oportuna, | |
| perder-se-á tudo que alega”. |
a) Quais aspectos do Arcadismo aparecem nessa caracterização?
b) Em que medida o poema de Cecília Meireles contradiz esses aspectos?
Ver questãoQuestão 82484
FUVEST
(FUVEST - 2024)
Na sua análise de O embarque para a ilha de Citera (cerca de 1712), de Antoine Watteau, Norbert Elias afirma que “em contraste com o jogo de luz e sombra claro-escuro enevoado que domina todo o quadro, está a luminosidade do sol poente, a radiante claridade à direita, no fundo. Isso confere um caráter de inquietude à composição. E, em contraste com a tranquilidade do antigo jardim com as copas verde-escuras das árvores e sua doce serenidade, a surda movimentação do cortejo dos amantes torna-se ainda mais intensa à medida que aqui, nessa claridade, os contornos de algo desconhecido, que não se deixa conhecer, perfis de construções que, precisamente por reluzirem como sombras através da névoa clara e radiosa, provocam um ligeiro arrepio, como sinal de perigo”.


a) Quais são as semelhanças entre a tela de Watteau e a Lira X de Tomás Antonio Gonzaga?
b) De que forma é descrito o “personagem” do poema?
Ver questãoQuestão 82485
FUVEST
(FUVEST - 2024)
Considerando as ideias apresentadas nos textos e também outras informações que julgar pertinentes, redija uma dissertação em prosa, na qual você exponha seu ponto de vista sobre o tema: Educação básica e formação profissional: entre a multitarefa e a reflexão.
Instruções:
- A dissertação deve ser redigida de acordo com a norma padrão da língua portuguesa.
- Escreva, no mínimo, 20 linhas, com letra legível, e não ultrapasse a quantidade de linhas disponíveis na folha de redação.
Texto 1
A multitarefa não é uma capacidade para a qual só seria capaz o homem na sociedade trabalhista e de informação pós-moderna. Trata-se antes de um retrocesso. A multitarefa está amplamente disseminada entre os animais em estado selvagem. Trata-se de uma técnica de atenção, indispensável para sobreviver na vida selvagem. Um animal ocupado no exercício da mastigação de sua comida tem de ocupar-se ao mesmo tempo também com outras atividades. Deve cuidar para que, ao comer, ele próprio não acabe comido. Ao mesmo tempo tem de vigiar sua prole e manter o olho em seu(sua) parceiro(a). O animal não pode mergulhar contemplativamente no que tem diante de si, pois tem de elaborar ao mesmo tempo o que tem atrás de si. Não apenas a multitarefa, mas também atividades como jogos de computador geram uma atenção ampla, mas rasa, que se assemelha à atenção de um animal selvagem.
Byung-Chul Han, Sociedade do cansaço. Adaptado.
Texto 2
Educar para o ócio significa ensinar a escolher um filme, uma peça de teatro, um livro. Ensinar como pode estar bem sozinho, consigo mesmo, significa também se habituar às atividades domésticas e à produção autônoma de muitas coisas que até o momento comprávamos prontas. Ensinar o prazer do convívio, da introspecção, do jogo e da beleza. Inculcar a alegria. A pedagogia do ócio também tem sua própria ética, sua estética, sua dinâmica e suas técnicas. E tudo isso deve ser ensinado. O ócio requer uma escolha atenta dos lugares justos: para se repousar, para se distrair e para se divertir. Portanto, é preciso ensinar aos jovens não só como se virar nos meandros do trabalho, mas também pelos meandros dos vários possíveis lazeres. Significa educar para a solidão e para o convívio, para a solidariedade e o voluntariado. Significa ensinar como evitar a alienação que pode ser provocada pelo tempo livre, tão perigosa quanto a alienação derivada do trabalho. Há muito o que ensinar!
Domenico de Masi. O ócio criativo.
Texto 3
Analisar as diferenças entre a educação escolar indígena e a educação escolar convencional no Brasil foi o ponto de partida do trabalho feito pelos pesquisadores Aline Abbonizio, da Universidade Federal Rural do Rio de Janeiro (UFRRJ), e Elie Ghanem, da Faculdade de Educação da Universidade de São Paulo (FEUSP). “Dois fatos me impressionaram especialmente na comunidade em que pesquisei, além do grande valor atribuído à escola como fator de fortalecimento da língua e da cultura daquele povo, a acentuada integração entre as atividades escolares e as práticas comunitárias. Não há tempos rígidos, não há horários fixos nem se seguem disciplinas escolares. As atividades da escola obedecem a um ritmo sereno e envolvem tarefas de manutenção dos costumes, incluem tanto a roça quanto o artesanato ou a coleta de produtos da mata”, relata Ghanem.
https://www4.fe.usp.br/pesquisa-da-feusp-analisa-diferencas-entre-educacao-indigena-e-convencional. Adaptado.
Texto 4

Texto 5

Texto 6

Texto 7

Questão 82486
FUVEST
(FUVEST - 2024)
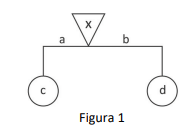
Um móbile matemático é uma figura que simula móbiles físicos. Ela é formada por segmentos de reta e figuras planas com valores numéricos racionais positivos, de forma a buscar um equilíbrio. A figura 1 ilustra um móbile básico matemático. Para ele estar em equilíbrio, os valores devem cumprir as equações e
. Quando não aparecem valores para as letras a e b, significa que ambas valem 1.
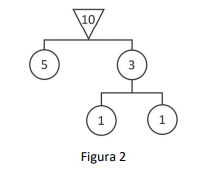
Um móbile pode ser composto por diversos móbiles básicos, como a figura 2. Note que, nele, tem-se , mantendo o móbile em equilíbrio.
Considerando os móbiles I, II e III, apresentados na folha de respostas, responda ao que se pede:
a) Complete o móbile I, preenchendo as formas geométricas vazias com os valores que faltam para que ele esteja em equilíbrio.
b) Determine para que o móbile II esteja em equilíbrio. c) Complete o móbile III, preenchendo as formas geométricas vazias com os valores que faltam para que ele esteja em equilíbrio.
Questão 82487
FUVEST
(FUVEST - 2024)
Uma padaria faz parte de um movimento que pretende combater o desperdício de alimentos e vende com descontos seus produtos próximos à data de vencimento. São montados três tipos de kits: A (doces), B (salgados) e C (mistos). No momento da compra, um cliente deve indicar apenas uma preferência entre os kits A, B ou C, mas receberá um kit surpresa (A, B ou C), conforme a disponibilidade de produtos em promoção.
Sabendo que 40% dos consumidores preferem o kit A, 30% preferem o kit B e 40% preferem o kit C e que a probabilidade de um cliente ter a sua preferência atendida é de 80% para o kit A, 90% para o kit B e 70% para o kit C, responda:
a) Qual a probabilidade de um cliente não ter a sua preferência atendida?
b) Dois amigos fazem uma compra cada um, indicando preferências distintas entre si. Qual a probabilidade de ambos terem as suas preferências atendidas?
c) Um cliente teve a sua preferência atendida. Qual a probabilidade de que ele tenha pedido o kit B?
Ver questãoQuestão 82488
FUVEST
(FUVEST - 2024)
Considere a parábola 𝑃 dada pela equação e a reta 𝑟 dada pela equação
, onde a, b e c são constantes reais. Denote por
a origem do sistema de coordenadas cartesiano
.
a) Se ,
e
, determine todos os pontos do plano cartesiano que pertencem, simultaneamente, à reta r e à parábola P.
b) Se ,
e
, determine o ponto da reta r que está mais próximo de 𝑂.
c) Considere três pontos A, B e C na parábola P, tais que , B pertence ao primeiro quadrante e os segmentos AB e 0C são paralelos. Determine B e C de forma que a distância de B até C seja
.
Questão 82489
FUVEST
(FUVEST - 2024)
Vamos admitir que uma corda presa nas extremidades de duas hastes paralelas e de mesma altura descreve uma curva que é dada pela equação . Uma representação gráfica dessa equação, limitada por duas retas verticais paralelas ao eixo
e onde o eixo
indica o solo, é dada pela figura. A unidade de medida é o metro (m).
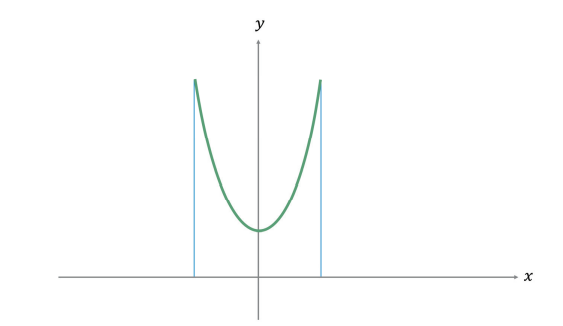
a) Qual a altura mais baixa que a corda assume?
b) Qual será a altura das hastes se a distância entre elas for de 3 m?
c) Qual a distância entre dois pontos da corda que estão a uma altura de 4 m do solo?
Ver questãoQuestão 82490
FUVEST
(FUVEST - 2024)
A figura a seguir esboça, no plano cartesiano, a região hachurada delimitada pelo eixo , pelo eixo
e pela reta
.
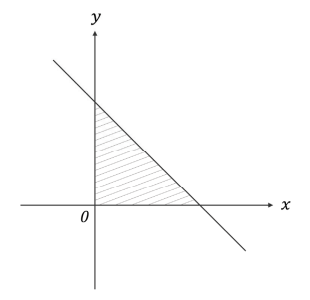
a) Calcule a área da região determinada pela intersecção do plano com o sólido de revolução gerado pela rotação da região hachurada quando gira em torno do eixo
.
b) Calcule o volume do sólido de revolução gerado pela rotação da região hachurada quando gira em torno da reta vertical .
c) Calcule o volume do sólido de revolução gerado pela rotação da região hachurada quando gira em torno da reta .
Questão 82491
FUVEST
(FUVEST - 2024)
Em matemática, define-se o piso de um número real x como sendo o maior número inteiro menor ou igual a x. O símbolo para o piso de x é . Por exemplo:
;
;
;
.
a) Determine x tal que .
b) Determine todas as soluções reais da equação .
c) Determine todas as soluções reais da equação .