FUVEST 2011

Questão 49308

(UNICAMP - 2011) 

Pensando nos pares amorosos, já se afirmou que “há n’O cortiço um pouco de Iracema coada pelo Naturalismo.”

(Antonio Candido, “De cortiço em cortiço”, em O discurso e a cidade. São Paulo: Duas Cidades, 1993, p.142.)

Partindo desse comentário, leia o trecho abaixo e responda às questões.

O chorado arrastava-os a todos, despoticamente, desesperando aos que não sabiam dançar. Mas, ninguém como a Rita; só ela, só aquele demônio, tinha o mágico segredo daqueles movimentos de cobra amaldiçoada; aqueles requebros que não podiam ser sem o cheiro que a mulata soltava de si e sem aquela voz doce, quebrada, harmoniosa, arrogante, meiga e suplicante. (...) Naquela mulata estava o grande mistério, a síntese das impressões que ele recebeu chegando aqui: ela era a luz ardente do meio-dia; ela era o calor vermelho das sestas da fazenda; era o aroma quente dos trevos e das baunilhas, que o atordoara nas matas brasileiras; era a palmeira virginal e esquiva que se não torce a nenhuma outra planta; era o veneno e era o açúcar gostoso; era o sapoti mais doce que o mel e era a castanha do caju, que abre feridas com o seu azeite de fogo; ela era a cobra verde e traiçoeira, a lagarta viscosa, a muriçoca doida, que esvoaçava havia muito tempo em torno do corpo dele, assanhando-lhe os desejos, acordando-lhe as fibras embambecidas pela saudade da terra, picandolhe as artérias, para lhe cuspir dentro do sangue uma centelha daquele amor setentrional, uma nota daquela música feita de gemidos de prazer, uma larva daquela nuvem de cantáridas que zumbiam em torno da Rita Baiana e espalhavam-se pelo ar numa fosforescência afrodisíaca. Isto era o que Jerônimo sentia, mas o que o tonto não podia conceber. De todas as impressões daquele resto de domingo só lhe ficou no espírito o entorpecimento de uma desconhecida embriaguez, não de vinho, mas de mel chuchurreado no cálice de flores americanas, dessas muito alvas, cheirosas e úmidas, que ele na fazenda via debruçadas confidencialmente sobre os limosos pântanos sombrios, onde as oiticicas trescalam um aroma que entristece de saudade. (...) E ela só foi ter com ele, levando-lhe a chávena fumegante da perfumosa bebida que tinha sido a mensageira dos seus amores; assentou-se ao rebordo da cama e, segurando com uma das mãos o pires, e com a outra a xícara, ajudava-o a beber, gole por gole, enquanto seus olhos o acarinhavam, cintilantes de impaciência no antegozo daquele primeiro enlace.

Depois, atirou fora a saia e, só de camisa, lançou-se contra o seu amado, num frenesi de desejo doido.

(Aluísio Azevedo, O Cortiço. Ficção Completa. Rio de Janeiro: Nova Aguilar, 2005, p. 498 e 581.)

a) Na descrição acima, identifique dois aspectos que permitem aproximar Rita Baiana de Iracema, mostrando os limites dessa semelhança.

b) Identifique uma semelhança e uma diferença entre Jerônimo e Martim.

Questão 49309

(UNICAMP - 2011) Uma empresa imprime cerca de 12.000 páginas de relatórios por mês, usando uma impressora jato de tinta colorida. Excluindo a amortização do valor da impressora, o custo de impressão depende do preço do papel e dos cartuchos de tinta. A resma de papel (500 folhas) custa R$ 10,00. Já o preço e o rendimento aproximado dos cartuchos de tinta da impressora são dados na tabela abaixo.

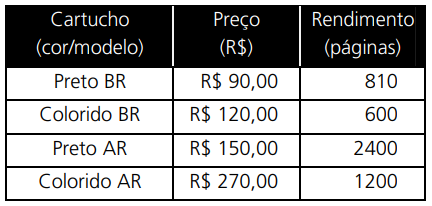
a) Qual cartucho preto e qual cartucho colorido a empresa deveria usar para o custo por página ser o menor possível?

b) Por razões logísticas, a empresa usa apenas cartuchos de alto rendimento (os modelos do tipo AR) e imprime apenas em um lado do papel (ou seja, não há impressão no verso das folhas). Se 20% das páginas dos relatórios são coloridas, quanto a empresa gasta mensalmente com impressão, excluindo a amortização da impressora? Suponha, para simplificar, que as páginas coloridas consomem apenas o cartucho colorido

Questão 49310

(UNICAMP - 2011) Uma grande preocupação atual é a poluição, particularmente aquela emitida pelo crescente número de veículos automotores circulando no planeta. Ao funcionar, o motor de um carro queima combustível, gerando CO₂, além de outros gases e resíduos poluentes.

a) Considere um carro que, trafegando a uma determinada velocidade constante, emite 2,7 kg de CO₂ a cada litro de combustível que consome. Nesse caso, quantos quilogramas de CO₂ ele emitiu em uma viagem de 378 km, sabendo que fez 13,5 km por litro de gasolina nesse percurso?

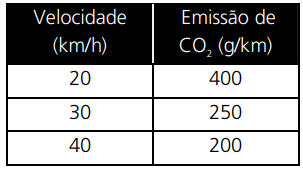
b) A quantidade de CO₂ produzida por quilômetro percorrido depende da velocidade do carro. Suponha que, para o carro em questão, a função c(v) que fornece a quantidade de CO₂, em g/km, com relação à velocidade v, para velocidades entre 20 e 40 km/h, seja dada por um polinômio do segundo grau. Determine esse polinômio com base nos dados da tabela abaixo.

Questão 49311

(UNICAMP - 2011) O perfil lipídico é um exame médico que avalia a dosagem dos quatro tipos principais de gorduras (lipídios) no sangue: colesterol total (CT), colesterol HDL (conhecido como “bom colesterol”), colesterol LDL (o “mau colesterol”) e triglicérides (TG). Os valores desses quatro indicadores estão relacionados pela fórmula de Friedewald: CT = LDL + HDL + TG/5. A tabela abaixo mostra os valores normais dos lipídios sanguíneos para um adulto, segundo o laboratório SangueBom.

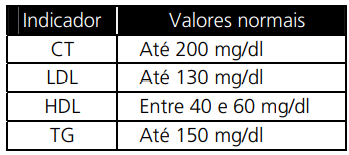
a) O perfil lipídico de Pedro revelou que sua dosagem de colesterol total era igual a 198 mg/dl, e que a de triglicérides era igual a 130 mg/dl. Sabendo que todos os seus indicadores estavam normais, qual o intervalo possível para o seu nível de LDL?

b) Acidentalmente, o laboratório SangueBom deixou de etiquetar as amostras de sangue de cinco pessoas. Determine de quantos modos diferentes seria possível relacionar essas amostras às pessoas, sem qualquer informação adicional. Na tentativa de evitar que todos os exames fossem refeitos, o laboratório analisou o tipo sanguíneo das amostras, e detectou que três delas eram de sangue O+ e as duas restantes eram de sangue A+. Nesse caso, supondo que cada pessoa indicasse seu tipo sanguíneo, de quantas maneiras diferentes seria possível relacionar as amostras de sangue às pessoas?

Questão 49312

(UNICAMP - 2011) Um grupo de pessoas resolveu encomendar cachorros-quentes para o lanche. Entretanto, a lanchonete enviou apenas 15 sachês de mostarda e 17 de catchup, o que não é suficiente para que cada membro do grupo receba um sachê de cada molho. Desta forma, podemos considerar que há três subgrupos: um formado pelas pessoas que ganharão apenas um sachê de mostarda, outro por aquelas que ganharão apenas um sachê de catchup, e o terceiro pelas que receberão um sachê de cada molho.

a) Sabendo que, para que cada pessoa ganhe ao menos um sachê, 14 delas devem receber apenas um dos molhos, determine o número de pessoas do grupo.

b) Felizmente, somente 19 pessoas desse grupo quiseram usar os molhos. Assim, os sachês serão distribuídos aleatoriamente entre essas pessoas, de modo que cada uma receba ao menos um sachê. Nesse caso, determine a probabilidade de que uma pessoa receba um sachê de cada molho.

Questão 49313

(UNICAMP - 2011 )No mês corrente, uma empresa registrou uma receita de R$ 600 mil e uma despesa de R$ 800 mil. A empresa estuda, agora, alternativas para voltar a ter lucro.

a) Primeiramente, assuma que a receita não variará nos próximos meses, e que as despesas serão reduzidas, mensalmente, em exatos R$ 45 mil. Escreva a expressão do termo geral da progressão aritmética que fornece o valor da despesa em função de n, o número de meses transcorridos, considerando como mês inicial o corrente. Calcule em quantos meses a despesa será menor que a receita.

b) Suponha, agora, que a receita aumentará 10% a cada mês, ou seja, que a receita obedecerá a uma progressão geométrica (PG) de razão 11/10. Nesse caso, escreva a expressão do termo geral dessa PG em função de n, o número de meses transcorridos, considerando como mês inicial o corrente. Determine qual será a receita acumulada em 10 meses. Se necessário, use 1,1² = 1,21; 1,1³ ≈ 1,33 e 1,1⁵ ≈ 1,61.

Questão 49314

(UNICAMP - 2011) Define-se como ponto fixo de uma função f o número real x tal que f(x) = x. Seja dada a função

a) Calcule os pontos fixos de f(x).

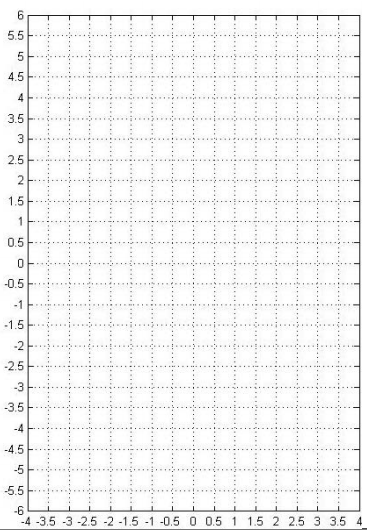
b) Na região quadriculada abaixo, represente o gráfico da função f(x) e o gráfico de g(x) = x, indicando explicitamente os pontos calculados no item (a).

Questão 49315

(UNICAMP - 2011) Considere uma gangorra composta por uma tábua de 240 cm de comprimento, equilibrada, em seu ponto central, sobre uma estrutura na forma de um prisma cuja base é um triângulo equilátero de altura igual a 60 cm, como mostra a figura. Suponha que a gangorra esteja instalada sobre um piso perfeitamente horizontal.

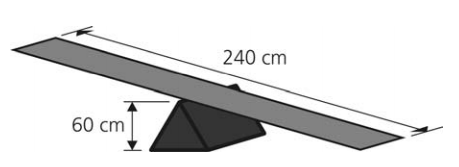
a) Desprezando a espessura da tábua e supondo que a extremidade direita da gangorra está a 20cm do chão, determine a altura da extremidade esquerda.

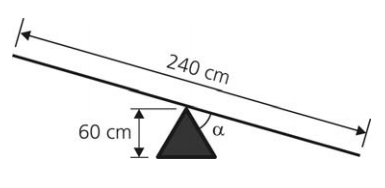
b) Supondo, agora, que a extremidade direita da tábua toca o chão, determine o ângulo α formado entre a tábua e a lateral mais próxima do prisma, como mostra a vista lateral da gangorra, exibida abaixo.

Questão 49316

(UNICAMP - 2011) Uma placa retangular de madeira, com dimensões 10 x 20 cm, deve ser recortada conforme mostra a figura ao lado. Depois de efetuado o recorte, as coordenadas do centro de gravidade da placa (em função da medida w) serão dadas por

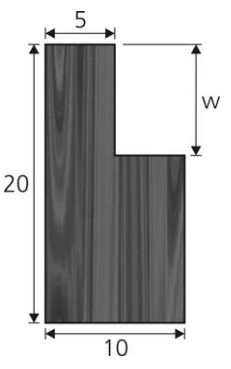
em que  é a coordenada horizontal e  é a coordenada vertical do centro de gravidade, tomando o canto inferior esquerdo como a origem.

a) Defina A(w), a função que fornece a área da placa recortada em relação a w. Determine as coordenadas do centro de gravidade quando A(w) = 150 cm² .

b) Determine uma expressão geral para , a função que fornece a dimensão w em relação à coordenada , e calcule quando = 7/2 cm.

Questão 49317

(UNICAMP - 2011) Para certo modelo de computadores produzidos por uma empresa, o percentual dos processadores que apresentam falhas após T anos de uso é dado pela seguinte função:

a) Em quanto tempo 75% dos processadores de um lote desse modelo de computadores terão apresentado falhas?

b) Os novos computadores dessa empresa vêm com um processador menos suscetível a falhas. Para o modelo mais recente, embora o percentual de processadores que apresentam falhas também seja dado por uma função na forma , o percentual de processadores defeituosos após 10 anos de uso equivale a 1/4 do valor observado, nesse mesmo período, para o modelo antigo (ou seja, o valor obtido empregando-se a função P(T) acima). Determine, nesse caso, o valor da constante c. Se necessário, utilize log₂(7) ≈ 2,81.