FUVEST 2022

Questão 70265

(FUVEST - 2022 - 2ª fase)

Uma sequência de números naturais é construída da seguinte forma: seu primeiro termo é escolhido como sendo um número natural qualquer. Se for par, então  e, se  for ímpar, então . Os termos seguintes  são obtidos de acordo com essa mesma regra. Por exemplo, se , então , ,  e assim por diante.

Dessa forma, a partir de , , a sequência  é definida como

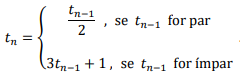
a) Para = 22, determine .

b) Determine todos os possíveis 𝑡ଵ para os quais .

c) Para , determine .

Questão 70266

(FUVEST - 2022 - 2ª FASE)

As afirmações a seguir baseiam-se na descrição da CETESB (Companhia Ambiental do Estado de São Paulo):

Afirmação 1: “O dióxido de enxofre (SO₂) é liberado para a atmosfera por gases vulcânicos e fontes antropogênicas, principalmente atividades industriais que processam materiais contendo enxofre, como termelétricas, fabricação de fertilizantes, fundição de alumínio e aço, produção de ácido sulfúrico e papel.”

Afirmação 2: “O dióxido de enxofre é um gás incolor com forte odor pungente. É muito irritante quando em contato com superfícies úmidas, pois se transforma em trióxido de enxofre (SO₃) e passa rapidamente a ácido sulfúrico (H₂SO₄).”

a) Represente a estrutura de Lewis do dióxido de enxofre.

b) A afirmação 2 refere-se à formação da chuva ácida. Represente a reação balanceada da formação da chuva ácida a partir de SO₃ e a reação balanceada da chuva ácida com o carbonato de cálcio (CaCO₃), que é um dos componentes de construções que são danificadas por ela.

c) Considere uma determinada amostra de carvão que contém 1% em massa de enxofre. Quando esse carvão é queimado, o enxofre é convertido em dióxido de enxofre pela reação S(s) + O₂(g)→ SO₂(g). Para evitar a poluição do ar, este dióxido de enxofre pode ser tratado com óxido de cálcio para formar sulfito de cálcio, como representado pela reação SO₂(g) + CaO(s) → CaSO₃(s). Calcule a massa diária, em quilogramas, de CaO necessária para tratar o SO₂ em uma usina que consome 3,2 × 106 kg de carvão por dia.

Questão 70267

(FUVEST - 2022 - 2ª fase)

Considere, no plano cartesiano, a circunferência com centro no ponto (0 , 3) e com raio 2 e, para cada , , a parábola cuja equação é y = 𝑎x² + 1.

a) Para 𝑎 = −1, encontre o ponto comum entre a circunferência e a parábola.

b) Para 𝑎 = 1, apresente 3 pontos em comum entre a circunferência e a parábola.

c) Encontre todos os valores de 𝑎 para os quais a circunferência e a parábola possuam exatamente 3 pontos em comum.

Questão 70268

(FUVEST - 2022 - 2ª fase)

Uma pirâmide 𝐏 tem base quadrada  de lado medindo 1 𝑢. 𝑚., apoiada em um plano , e quatro faces que são triângulos equiláteros, ligando a base ao ápice de 𝐏. Os dezesseis pontos  e , indicados na figura, dividem cada aresta da pirâmide em três segmentos de igual medida.

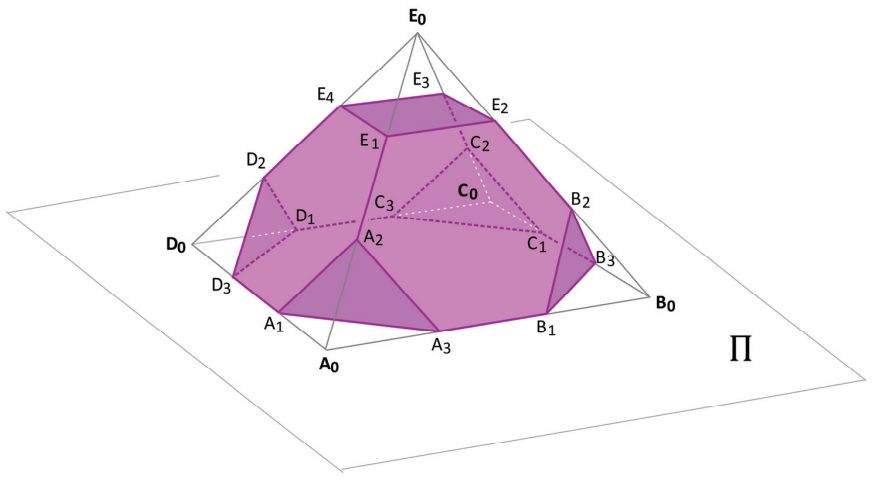
Um novo sólido 𝐒, em destaque na figura, é produzido subtraindo-se de 𝐏 as cinco pirâmides , , ,  e . Determine:

a) o perímetro da face de 𝐒 que se apoia em , cujos vértices são  e .
b) o volume de 𝐒.
c) a distância entre e . 

Questão 70269

(FUVEST - 2022 - 2ª fase)

Uma empresa distribuidora de alimentos tem latas de ervilha (E) e latas de milho (M), em dois pesos, 1 kg e 2kg, totalizando 4 (quatro) tipos de latas: E1 e E2 (ervilha, em pesos de 1kg e 2kg, respectivamente) e M1 e M2 (milho, em pesos de 1kg e 2kg, respectivamente). Essas latas são agrupadas em pacotes para envio aos comerciantes. Dois pacotes de latas são considerados iguais se contiverem a mesma quantidade de latas de cada tipo, independentemente da maneira como são organizadas no pacote.

a) Quantos pacotes diferentes pesando, cada um, exatamente 200kg (duzentos quilos) podem ser montados usando-se apenas latas dos tipos E1 e E2? Na contagem, deve-se também levar em conta pacotes formados por apenas 1 tipo dessas latas.

b) Quantos pacotes diferentes pesando, cada um, exatamente 200kg (duzentos quilos) podem ser montados usando-se apenas latas dos tipos E1, E2 e M1? Na contagem, deve-se também levar em conta pacotes formados por apenas 1 ou 2 tipos dessas latas.

c) Quantos pacotes diferentes pesando, cada um, exatamente 20kg (vinte quilos) podem ser montados usando-se latas dos tipos E1, E2, M1 e M2? Na contagem, deve-se também levar em conta pacotes formados por apenas 1, 2 ou 3 tipos dessas latas.

Questão 70270

(FUVEST - 2022 - 2ª fase)

O material publicitário apareceu em 1935 nas páginas do Almanaque Fontoura, distribuído gratuitamente nas farmácias e que reunia curiosidades e informações. A partir da leitura da propaganda, responda:

a) Qual o tema da propaganda?

b) Quem é o Jeca Tatu e que categoria social ele representa?

c) Aponte duas razões do emprego do personagem Jeca Tatu na propaganda.

Questão 70272

(FUVEST - 2022 - 2ª fase)

A conversão de energia mecânica das ondas do mar é uma promissora fonte alternativa de energia limpa, e vários protótipos têm sido desenvolvidos para este fim. Uma das possíveis aplicações é o uso de câmaras de ar pressurizadas que usem a oscilação das ondas do mar para fazer girar o eixo de um dínamo ou de uma turbina, gerando energia elétrica.

Considere o esquema mostrado na figura: uma boia flutua no mar e seu movimento vertical faz mover o pistão 1 de área A que comprime o ar em uma câmara pressurizada a uma pressão P₀. A distância máxima entre o pistão 1 e o topo da câmara é L. Um segundo pistão (pistão 2) de área A/10 colocado horizontalmente na lateral superior da câmara é acoplado a um mecanismo que faz girar um dínamo.

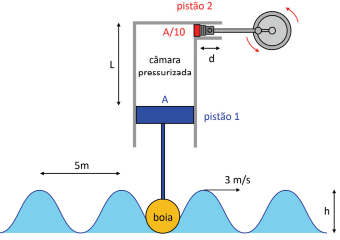
Considere inicialmente que ambos os pistões são livres para se movimentarem sem atrito e que a pressão e a temperatura do gás no interior da câmara não se alterem significativamente.

a) Se as ondas do mar forem ondas perfeitamente harmônicas com velocidade de 3 m/s e a distância entre as cristas for de 5 m, calcule o período de rotação do dínamo.

b) Se a amplitude das ondas do mar é h, calcule a distância horizontal máxima d percorrida pelo pistão 2.

Considere agora uma situação em que o gerador é desativado, travando-se o pistão 2, de modo que ele não possa se mover.

c) Calcule a pressão máxima na câmara considerando que a temperatura do gás em seu interior não varie. Expresse sua resposta em termos da pressão inicial na câmara P₀, e de L e h.

Note e adote:

Considere o gás no interior da câmara como sendo ideal e em equilíbrio termodinâmico em todas as etapas do processo.

Questão 70273

(FUVEST - 2022 - 2ª fase)

No dia 22 de agosto de 1988, o Governo Federal fundou a primeira instituição pública voltada para promoção e preservação dos valores culturais, históricos, sociais e econômicos decorrentes da influência negra na formação da sociedade brasileira: a Fundação Cultural Palmares (FCP), entidade vinculada ao Ministério da Cidadania. Ao longo dos anos, a FCP tem trabalhado para promover uma política cultural igualitária e inclusiva, que contribua para a valorização da história e das manifestações culturais e artísticas negras brasileiras como patrimônios nacionais.

“Apresentação”. www.palmares.gov.br

A partir da leitura do excerto e de seus conhecimentos sobre o tema:

a) Justifique o nome da instituição.

b) Identifique o contexto em que a instituição foi criada.

c) Cite duas políticas públicas, hoje vigentes no Brasil, que estejam em sintonia com as orientações dessa instituição mencionadas no texto.

Questão 70274

(FUVEST - 2022 - 2ª FASE)

Considere as substâncias cujas estruturas estão representadas a seguir:

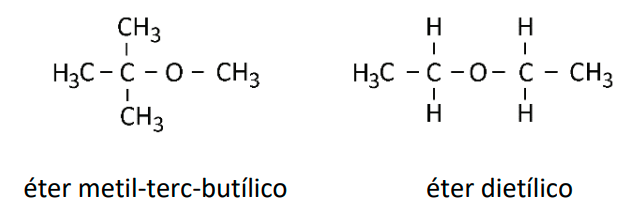
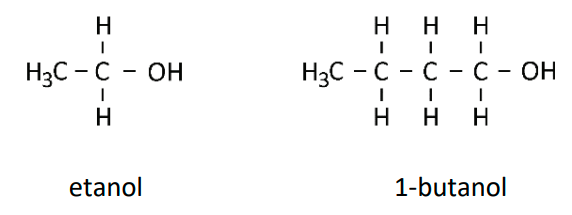
a) Considerando que tanto o etanol quanto o 1-butanol interagem por ligação de hidrogênio com a água, por que o etanol é mais solúvel em água do que o 1-butanol à mesma temperatura?

b) Escreva, no quadro da folha de respostas, as estruturas de dois álcoois que são isômeros do 1-butanol.

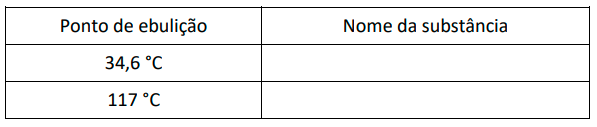
c) O 1-butanol e o éter dietílico são compostos que possuem a mesma fórmula química, C₄H₁₀O, porém pontos de ebulição diferentes, sendo que um deles entra em ebulição a 34,6 °C e o outro, a 117 °C a 1 atm. Preencha o quadro, na folha de respostas, relacionando os nomes das substâncias com os respectivos pontos de ebulição. Justifique sua resposta.

Quadro do item B:

Quadro do item C:

Questão 70275

(FUVEST - 2022 - 2ª fase)

À medida que a construção prosseguia, Rondon iniciava a segunda fase do seu projeto: a crucial exploração das terras da bacia amazônica onde hoje está situado o estado de Rondônia, pois a linha telegráfica atravessaria aquelas terras. Essa era a região que incendiava a imaginação de Rondon e seus oficiais, e também a de muitos brasileiros das cidades costeiras. Era o Brasil desconhecido. (...) Na verdade, o projeto do telégrafo parecia dar muito mais satisfação a Rondon pela chance de explorar aquelas terras do que pela construção da linha telegráfica (...) Rondon planejou uma expedição em 1907 para descobrir a nascente do rio Juruena e fazer contato com os indígenas conhecidos como nambikwara.

DIACON, Todd A. Rondon: o marechal da floresta. São Paulo: Companhia das Letras, 2006, p. 32-33.

a) Indique qual a importância da expansão da linha telegráfica no Brasil dessa época.

b) Explique o sentido da frase “Era o Brasil desconhecido”.

c) Caracterize a política indigenista desenvolvida por Cândido Rondon para “aquelas terras”.