ITA 2023

Questão 73724

(AFA - 2023)

Nas questões de Física, quando necessário, utilize:

• aceleração da gravidade: 
• 
• 
• calor específico da água: 
• calor latente de fusão do gelo: 
• temperatura de fusão do gelo: 
• densidade do gelo:
• densidade da água: 

O maior valor do campo elétrico que um dielétrico suporta, sem tornar-se condutor, é chamado rigidez dielétrica.

A rigidez dielétrica varia de material para material, e para o ar, em condições normais, é de .

O potencial máximo, em kV, para se manter carregada uma esfera metálica de 10 cm de diâmetro, imersa no ar, longe de quaisquer outros objetos, sem que ela descarregue, é igual a

Questão 73725

(AFA - 2023)

Nas questões de Física, quando necessário, utilize:

• aceleração da gravidade: 
• 
• 
• calor específico da água: 
• calor latente de fusão do gelo: 
• temperatura de fusão do gelo: 
• densidade do gelo:
• densidade da água: 

Três canaletas planas e horizontais, sendo as duas primeiras semicirculares e a terceira com perfil de um quarto de circunferência, são dispostas conforme figura a seguir. Nas entradas de cada canaleta encontram-se três partículas, A, B e C, de massas m, m e 2m, respectivamente.

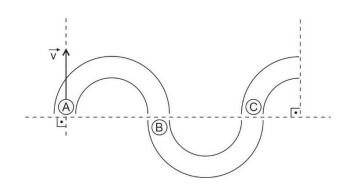
O sistema composto pelas canaletas e partículas é conservativo e todas as colisões são frontais, sendo que, entre A e B, perfeitamente elástica(s), e entre, B e C, parcialmente elástica(s), com coeficiente de restituição igual a 0,5.

No instante inicial, a partícula A é lançada com velocidade , e B e C estão em repouso, conforme indica a figura. O impulso sofrido pelo conjunto de partículas, desde o lançamento de A até a saída de C, na terceira canaleta, tem módulo igual a

Questão 73726

(AFA - 2023)

Nas questões de Física, quando necessário, utilize:

• aceleração da gravidade: 
• 
• 
• calor específico da água: 
• calor latente de fusão do gelo: 
• temperatura de fusão do gelo: 
• densidade do gelo:
• densidade da água: 

Uma partícula é lançada obliquamente e descreve um movimento parabólico, sem resistência do ar. No momento do lançamento dessa partícula, o vetor velocidade  faz o ângulo  com a horizontal e, ao atingir a altura máxima de sua trajetória, o vetor posição  da partícula faz um ângulo  com essa mesma horizontal, conforme ilustra figura a seguir:

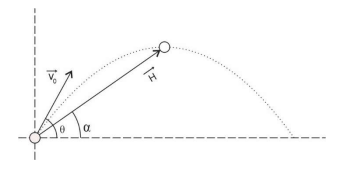
Nessas condições, a razão entre as tangentes de  e ,  , vale

Questão 73727

(AFA - 2023)

Nas questões de Física, quando necessário, utilize:

• aceleração da gravidade: 
• 
• 
• calor específico da água: 
• calor latente de fusão do gelo: 
• temperatura de fusão do gelo: 
• densidade do gelo:
• densidade da água: 

Por duas vezes, observa-se o movimento de um bloco, sem resistência do ar, sobre um plano inclinado, conforme ilustra figura seguinte:

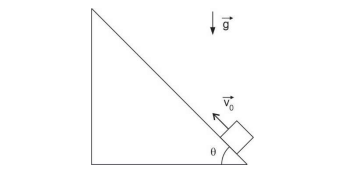
O coeficiente de atrito cinético entre as superfícies do bloco e do plano inclinado é .

No primeiro lançamento, em que , o tempo que o bloco gasta até parar, sobre o plano inclinado, é t. No segundo lançamento, que se dá com mesma velocidade inicial do primeiro, e o tempo gasto pelo bloco até parar, também sobre o plano inclinado, é t’.

Nessas condições, a razão entre os tempos  é igual a

Questão 73728

(AFA - 2023)

Nas questões de Física, quando necessário, utilize:

• aceleração da gravidade: 
• 
• 
• calor específico da água: 
• calor latente de fusão do gelo: 
• temperatura de fusão do gelo: 
• densidade do gelo:
• densidade da água: 

Uma cuba de ondas, de profundidade constante, contém água até a altura 20 cm.

A partir de determinado instante, dois estiletes, e , que funcionam como fontes de ondas circulares, vibrando em oposição de fase com frequência de 5 HZ , produzem ondas de amplitudes de 2 cm na superfície da água, que se propagam com velocidade de 10 cm/s.

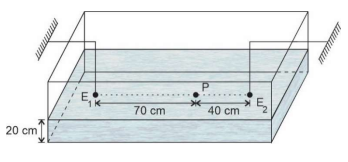
No ponto P, indicado na figura acima, uma rolha de cortiça ao ser atingida pelas duas ondas poderá ter sua posição vertical y, em função do tempo t, descrita pela equação

Questão 75973

(ITA - 2023 - 1ª FASE)

Uma partícula é lançada horizontalmente de uma determinada altura em relação ao solo em duas situações: uma em vácuo e outra em ar atmosférico estático, mantendo todas as outras características, como altura e velocidade inicial idênticas. O gráfico do módulo de sua velocidade v em função da distância horizontal x, no caso do lançamento no vácuo, é mostrado na figura pela curva em linha tracejada, juntamente com mais outras quatro curvas. O ponto no extremo de cada curva indica a posição em que a partícula atingiu o solo.

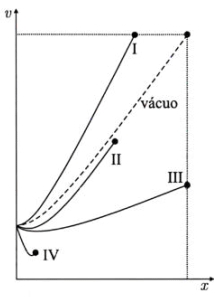
Pode(m) descrever de maneira correta o lançamento em ar atmosférico apenas a(s) curva(s)

Questão 75975

(ITA - 2023 - 1ª FASE)

Um disco de raio R com centro em O pode girar livremente em um plano horizontal sem atrito em torno de um eixo fixo que passa por O. Uma mola de comprimento natural L tem uma das suas extremidades articuladas a um ponto fixo na parede. Este ponto está localizado a uma distância L do ponto O. A outra extremidade está articulada à borda do disco, em uma posição cujo movimento será analisado a seguir. Inicialmente, a mola se encontra em orientação perpendicular à parede e seu comprimento está reduzido a x = L – R, como mostra a figura.

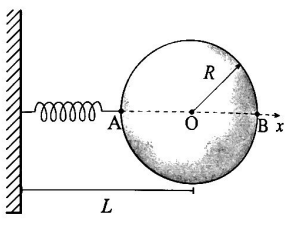
Considere que os pontos A e B são pontos fixos do espaço e que R < L. A seguir, são feitas algumas afirmações sobre esse sistema.

1. O sistema tem apenas dois pontos de equilíbrio, A e B, sendo ambos instáveis.

2. Se um pequeno torque impulsivo for aplicado ao disco, este último continuará completando voltas inde finidamente, contanto que não haja nenhuma dissipação de energia.

4. Se um pequeno torque impulsivo for aplicado ao disco, este pode não completar uma volta se a sua massa for muito grande e a constante elástica for muito pequena, mesmo sem haver dissipação de energia.

8. Seja C um ponto fixo no espaço a uma distância R de O. Se |AOC| < 30°, C nunca será um ponto de equilíbrio estável.

Assinale a alternativa que contém a soma dos números correspondentes às afirmações verdadeiras.

Questão 75977

(ITA - 2023 - 1ª FASE)

Considere um recipiente, sobre uma plataforma, sujeito à pressão atmosférica P_atm. Esse recipiente contém um volume inicial V_i de um gás monoatômico ideal em equilíbrio e tem um êmbolo de seção transversal de área A e de massa m. Para monitorar a aceleração do sistema, a plataforma foi suspensa por um dinamômetro, como ilustrado na figura. Por causa de uma ação de uma força externa vertical, o êmbolo atinge uma nova posição de equilíbrio. Nessa posição a leitura do dinamômetro indica que a aceleração do sistema é de 1/10 de g para cima.

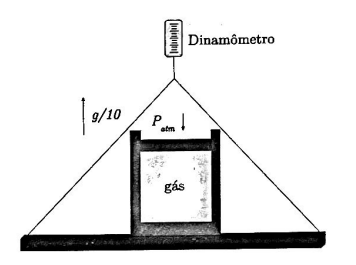
Determine o módulo do deslocamento Δx do êmbolo, com relação ao fundo do recipiente, considerando que a transformação do gás é isentrópica.

Questão 75979

(ITA - 2023 - 1ª FASE)

Um corpo de massa m é lançado em um plano horizontal sem atrito, sob ação da gravidade g, e, ao entrar em um tubo, executa uma trajetória circular de raio R. A força exercida no corpo pelo tubo logo após o início do movimento circular tem intensidade F. Após meia volta, o corpo percorre uma trajetória retílinea em movimento uniforme até certa distância e depois sobe até certa altura h. O corpo sai do tubo em movimento vertical e imediatamente passa a se mover dentro de um fluido viscoso até atingir altura máxima H, conforme mostra a figura.

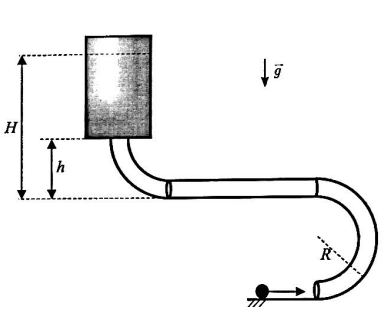
Considere que o corpo se desloca pelo tubo sem atrito; que o diâmetro do tubo é desprezível em relação a R, h e H; e que o módulo do trabalho realizado pela força de atrito viscoso até a massa atingir H é equivalente a um terço da energia cinética da partícula, quando esta adentra o fluido. Assinale a alternativa que expressa H em função das variáveis fornecidas.

Questão 75980

(ITA - 2023 - 1ª FASE)

Considere um recipiente tubular fino, com área transversal constante, que contém dois líquidos imissíveis A e B. As hastes verticais deste recipiente distam 20 cm uma da outra (L = 20 cm). Quando o recipiente está em repouso, o líquido A atinge uma altura de 80 cm em relação à linha de separação dos líquidos. Quando o recipiente é colocado em movimento retilíneo uniformemente variado, a altura de A com relação à linha de separação dos líquidos passa a ser H = 76 cm, conforme mostra a figura.

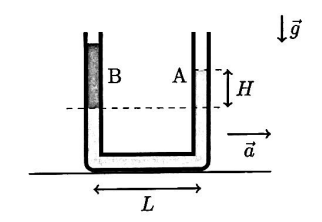
Considerando-se que o sistema parta do repouso, a distância percorrida pelo recipiente após um intervalo de 3,0 s é