FUVEST 2007

Questão 44702

(FUVEST - 2007 - 2 fase - Questão 2)

Na figura abaixo, os segmentos AB e CD são paralelos, o ângulo OÂB mede 120º , AO = 3 e AB = 2 . Sabendo-se ainda que a área do triângulo OCD vale  ,

a) calcule a área do triângulo OAB.

b) determine OC e CD.

Questão 44703

(FUVEST - 2007 - 2 fase - Questão 3)

Em uma progressão aritmética a₁, a₂, ..., a_n, ... a soma dos n primeiros termos é dada por S_n = bn² +  n, sendo b um número real. Sabendo-se que a₃ = 7, determine

a) o valor de b e a razão da progressão aritmética.

b) o 20^o termo da progressão.

c) a soma dos 20 primeiros termos da progressão.

Questão 44704

(FUVEST - 2007 - 2 fase - Questão 4)

A figura representa um trapézio ABCD de bases AB e CD, inscrito em uma circunferência cujo centro O está no interior do trapézio.

Sabe-se que AB = 4, CD = 2 e AC = .

a) Determine a altura do trapézio.

b) Calcule o raio da circunferência na qual ele está inscrito.

c) Calcule a área da região exterior ao trapézio e delimitada pela circunferência.

Questão 44705

(FUVEST - 2007 - 2 fase - Questão 5)

Um arco x está no terceiro quadrante do círculo trigonométrico e verifica a equação .

Determine os valores de sen x e cos x.

Questão 44706

(FUVEST - 2007 - 2 fase - Questão 6)

Na figura abaixo, os pontos A₁, A₂, A₃, A₄, A₅, A₆ são vértices de um hexágono regular de lado 3 com centro na origem O de um sistema de coordenadas no plano. Os vértices A₁ e A₄ pertencem ao eixo x. São dados também os pontos B = (2 ,0) e C = (0 ,1) .

Considere a reta que passa pela origem O e intersecta o segmento BC no ponto P, de modo que os triângulos OPB e OPC tenham a mesma área. Nessas condições, determine

a) a equação da reta OP .

b) os pontos de interseção da reta OP com o hexágono.

Questão 44707

(FUVEST - 2007 - 2 fase - Questão 7)

Uma urna contém 5 bolas brancas e 3 bolas pretas. Três bolas são retiradas ao acaso, sucessivamente, sem reposição. Determine

a) a probabilidade de que tenham sido retiradas 2 bolas pretas e 1 bola branca.

b) a probabilidade de que tenham sido retiradas 2 bolas pretas e 1 bola branca, sabendo-se que as três bolas retiradas não são da mesma cor.

Questão 44708

(FUVEST - 2007 - 2 fase - Questão 8)

Um castelo está cercado por uma vala cujas bordas são dois círculos concêntricos de raios 41 m e 45 m. A profundidade da vala é constante e igual a 3 m.

O proprietário decidiu enchê-la com água e, para este fim, contratou caminhões-pipa, cujos reservatórios são cilindros circulares retos com raio da base de 1,5 m e altura igual a 8 m.

Determine o número mínimo de caminhões-pipa necessário para encher completamente a vala.

Questão 44709

(FUVEST - 2007 - 2 fase - Questão 9)

a) Represente, no sistema de coordenadas, os gráficos das funções  e 

b) Resolva a inequação 

Questão 44710

(FUVEST - 2007 - 2 fase - Questão 10)

O cubo ABCDEFGH possui arestas de comprimento a. O ponto M está na aresta AE e AM = 3 ⋅ ME.

Calcule:

a) O volume do tetraedro BCGM.

b) A área do triângulo BCM.

c) A distância do ponto B à reta suporte do segmento CM .

Questão 44767

(FUVEST - 2007 - 2 fase - Questão 2)

Em 1912, François Auguste Victor Grignard recebeu o prêmio Nobel de Química pela preparação de uma nova classe de compostos contendo, além de carbono e hidrogênio, magnésio e um halogênio – os quais passaram a ser denominados “compostos de Grignard”. Tais compostos podem ser preparados pela reação de um haleto de alquila com magnésio em solvente adequado.

Os compostos de Grignard reagem com compostos carbonílicos (aldeídos e cetonas), formando álcoois. Nessa reação, forma-se um composto intermediário que, reagindo com água, produz o álcool.

​​​​​​

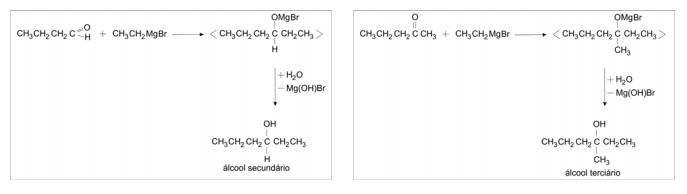
Por este método, para preparar o álcool terciário

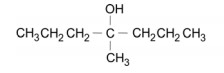
há duas possibilidades de escolha dos reagentes. Preencha a tabela da folha de respostas ao lado para cada uma delas.

Folha de respostas: