ITA 2021

Questão 66709

Um planeta perfeitamente esférico e de raio R tem aceleração da gravidade g em sua superfície. A aceleração da gravidade, em um ponto que está a uma altura h da superfície desse planeta, vale:

Questão 66965

(IME - 2021/2022)

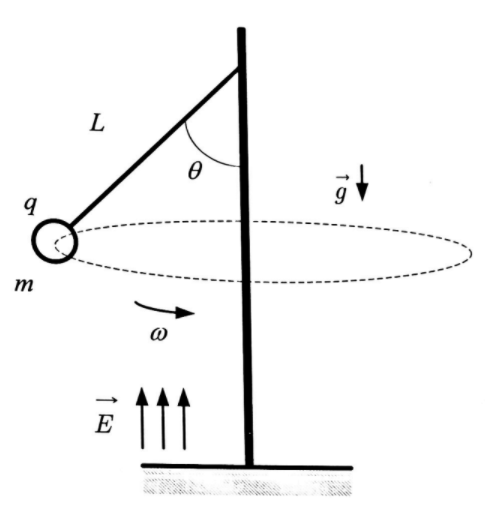
A figura mostra uma pequena esfera carregada, interligada por um cabo de comprimento L, inextensível e de massa desprezível, que gira em torno de um eixo vertical com velocidade angular . 

O movimento da esfera ocorre numa região submetida a um campo elétrico uniforme , conforme indicado na figura.

Dados:

• massa da esfera: m = 50g;
• carga elétrica da esfera: q = -10 C;
• Intensidade do campo elétrico: || = 0,07 N/C;
• velocidade angular do eixo:  = 120 rpm;
• comprimento do cabo: L = 30 cm;
• aceleração da gravidade: g = 10 m/s²; e
• .

Observação:

• a espessura do eixo vertical é desprezível.

O ângulo  formado entre o cabo e o eixo é aproximadamente:

Questão 66966

(IME - 2021/2022)

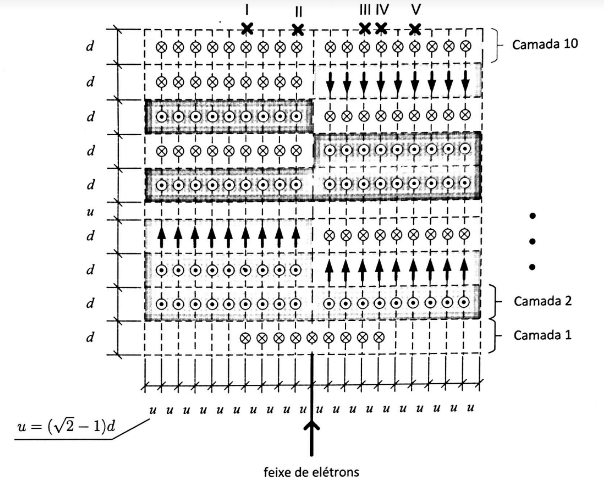
Um feixe de elétrons penetra em uma região, dividida em camadas espaçadas de acordo com as dimensões mostradas na figura, que está sujeita a um campo magnético heterogêneo. Em cada camada, a direção e o sentido do campo magnético mudam (vide figura), mas seu módulo será sempre constante. Note que na figura existem áreas desprovidas de campo magnético. Sabendo que, após passar pela primeira camada, o feixe descreve um arco de 1/8 de circunferência, ele sairá na camada 10 no ponto: 

Questão 66967

(IME - 2021/2022)

Seja  o conjunto de todos os valores de  para os quais a soma dos termos da progressão

assume um valor finito. Define-se a função , para cada , tal que

A soma das raízes da equação , é:

Questão 66968

(IME - 2021/2022)

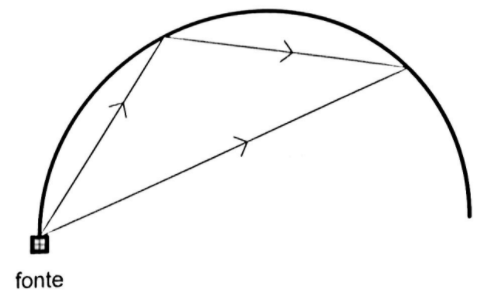
Conforme ilustrado na figura, uma fonte localizada na extremidade de um anteparo, que é reflexivo e tem a forma de uma semi-circunferência, emite raios luminosos de comprimento de onda constante, em fase, em todas as direções;

Observações:

• para cada ponto da semi-circunferência, considere apenas o efeito da interferência de uma única reflexão, como exemplificação na figura; e
• considere que, na reflexão, o raio luminoso sofra uma inversão de fase.

Sabendo que a razão entre o raio da semi-circunferência e o comprimento de onda é 30, o número N de máximos locais de interferência que serão observados no anteparo é tal que:

Questão 66970

(IME - 2021/2022 - 1ª fase)

Uma reação entre dois líquidos A e B produz dois compostos gasosos C e D, de acordo com a estequiometria A + B → C + D. Se conduzida a pressão e temperatura constantes, pode-se afirmar que:

Questão 66971

(IME - 2021/2022)

Quantos pares ordenados (x, y) de números inteiros satisfazem a equação 1/x + 1/y = 1/23?

Questão 66972

(IME - 2021/2022 - 1ª fase)

Na desidratação a alta temperatura de uma mistura reacional composta pelos ácidos fórmico, acético e propiônico, qual a quantidade máxima de diferentes anidridos que poderá ser obtidos?

Questão 66973

(IME - 2021/2022 - 1ª fase)

Considere a seguinte reação em equilíbrio: 

2SO₂ (g) + O₂ (g)  2SO₂ (g)

Dados:

• R = 8,3 J. (K.mol)^-1;
• In 1,6 = 0,47; e 
• In 10 = 2,3.

Sabe-se que a constante de equilíbrio dessa reação é 4,0.10²⁴, a 27 ºC e 2,5.10¹⁰, a 227 ºC. Qual a variação de entalpia padrão da reação, em kJ.mol^-1, considerando que ela seja constante nessa faixa de temperatura? 

Questão 66974

(IME - 2021/2022)

Considere o conjunto de todas as retas que são secantes ao gráfico da função

e que passam pelo ponto 

O menor valor dentre os coeficientes angulares das retas desse conjunto é: