ITA 2021

Questão 67302

(IME - 2021/2022 - 2ª fase) 

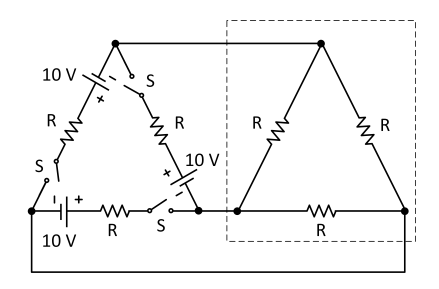
A figura acima apresenta um circuito composto por três baterias de 10 V, seis resistores idênticos R e três chaves S.

Ao fechar as três chaves simultaneamente, após 20 segundos, o circuito consome 20 kJ de energia.

Considerando sempre a topologia do circuito original para cada pedido, determine:

a) o valor da resistência de cada resistor R, em Ω;

b) a potência dissipada no circuito, em W, se 01 (uma) das baterias tiver seus terminais curto-circuitados; e

c) a potência dissipada no circuito, em W, se os três resistores da região tracejada do circuito tiverem seus terminais abertos.

Questão 67303

(IME - 2021/2022 - 2ª fase) O interior de um refrigerador hospitalar para armazenagem de medicamentos deve ser continuamente mantido a uma temperatura de 2 ºC. Este equipamento possui três portas envidraçadas para acesso aos fármacos, sendo por isso afetado pelo calor ambiente. Além disso, estima-se que os outros ganhos térmicos pelas demais superfícies são equivalentes a 20% daquele associado ao total das três portas.
A superintendência do hospital contratou uma empresa para elaborar o projeto de um sistema alternativo de fornecimento de energia elétrica, em caso de interrupção do serviço pela concessionária local. Após estudo, o técnico responsável pelo projeto afirmou que:

“A potência de acionamento do refrigerador hospitalar é suprida com folga por um motor térmico operando em um ciclo termodinâmico que possui as seguintes características: o motor recebe energia de uma fonte, cuja temperatura é 327 ºC, e rejeita energia para outras duas fontes. Uma dessas fontes se encontra à temperatura externa ao refrigerador e recebe 450 W, enquanto a outra deve estar a uma temperatura de 127 ºC, recebendo 300 W.”

Dados:
• condutividade térmica do vidro: 0,85 W.(m.ºC)⁻¹;
• espessura do vidro: 25 mm;
• temperatura do ambiente externo ao refrigerador: 27 ºC;
• coeficiente de desempenho do refrigerador:  do máximo admissível do ciclo de Carnot associado; e
• dimensões de cada porta de vidro: 2 m (altura) x 50 cm (largura).

A partir de uma análise termodinâmica da situação, explique, de forma justificada, se a afirmação do técnico é correta.

Questão 67304

(IME - 2021/2022 - 2ª fase) 

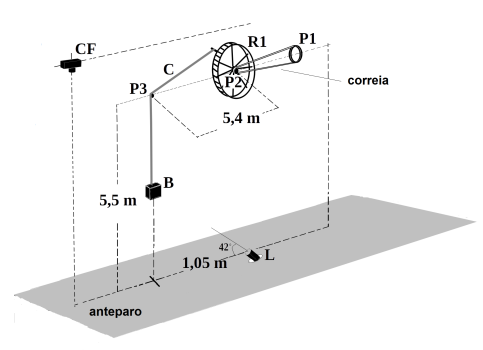
Seja o sistema composto por polias P1, P2 e P3, uma roda R1, uma corda inextensível C, um cubo B, um laser L e uma câmera fotográfica CF, dispostos conforme a figura acima. Nesse sistema, a face inferior do cubo B é reflexiva e pode ser considerada um espelho plano ideal. Tanto as polias quanto a roda estão fixadas em suas posições, de tal modo que podem girar livremente no plano que contém seus centros e a corda C. As polias P1 e P2 estão ligadas por uma correia, que corre sem deslizar, e a polia P2 e a roda R1 sao concêntricas. A câmera fotográfica CF registra fotos do anteparo, a uma taxa de cinco fotos por segundo. Sabe-se que a velocidade angular da polia P1 só pode assumir valores inteiros de 1 ate 10 rad/s, e que a primeira foto mostra um ponto luminoso.

Dados:

• raio de P1: 40 cm;

• raio de P2: 3,14 cm;

• raio de P3: desprezível;

• raio de R1: 90 cm;

• comprimento de C: 9 m;

• aresta do cubo B: 10 cm;

• tg(42º) = 0,90;

• π = 3,14; e

• π² = 10

Determine quais valores de velocidade angular da polia P1, em rad/s, farão com que todas as fotos tiradas pela câmara sejam iguais.

Questão 67305

(IME - 2021/2022 - 2ª fase)

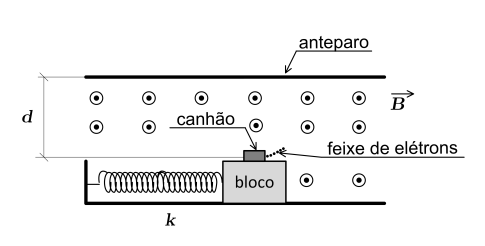
Na figura, encontra-se ilustrado um experimento, em que o canhão preso ao bloco efetua um movimento harmônico simples (MHS) na região sujeita ao campo magnético constante, disparando horizontalmente e continuamente um feixe de elétrons. Nele, observou-se que, nos momentos em que o bloco está com a maior energia cinética, ora os elétrons colidem ortogonalmente contra o anteparo, ora colidem frontalmente contra a traseira do canhão, após tangenciarem o anteparo.

Dados:

• velocidade relativa de disparo do feixe de eletrons em relação ao canhão: ;
• constante elástica da mola: ;
• massa do conjunto bloco + canhão: ;
• carga do elétron: ;
• massa do elétron: ;
• distância entre o canhão e o anteparo: .

Determine:

a) a amplitude de oscilação do bloco para que o experimento seja viável, em função de ,  e ;

b) o ângulo de impacto entre o anteparo e os elétrons disparados quando o bloco estiver com velocidade nula;

c) a densidade de fluxo magnético do campo , para que o experimento seja viável, em função de ,  ,  e ;

d) os possíveis valores de  em relação a , e impostos pelo tempo de viagem dos eletrons até o choque frontal com a traseira do canhão.

Questão 67306

(IME - 2021/2022 - 2ª fase) 

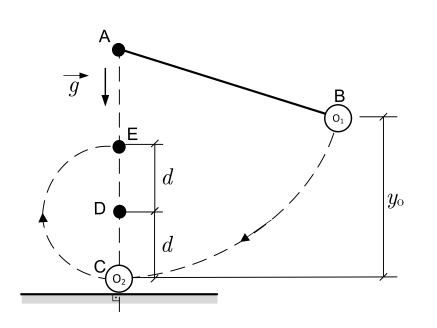
Um objeto O₁, preso por um fio ideal, e solto do ponto B. Ao atingir o ponto C, ele se choca de forma totalmente inelástica, colando no objeto O₂, conforme ilustrado na figura. Após o choque, o fio encontra o ponto D, que passa a ser o novo centro do movimento pendular do conjunto O₁ + O₂.

Dados:

• aceleração da gravidade: g;

• massa de O₁ = m₁; e

• massa de O₂ = m₂.

Observações:

• considere que os objetos sao partículas; e

• desprezar os atritos e a resistência do ar.

Diante do exposto, determine:

a) a distância y_o mínima indicada na figura, em função de d, m₁, m₂ e g, de modo que o conjunto consiga atingir o ponto E;

b) a velocidade do conjunto O₁ + O₂ no ponto E, nas condições do item a; e 

c) a tração do fio no ponto C, imediatamente após o choque, nas condições do item a.

Questão 67307

(IME - 2021/2022 - 2ª fase) 

A ponte acima é escorada por quatro apoios verticais (A, B, E e F) e por dois engates (C e D), que permitem a transmissão de esforços verticais e horizontais. Um veículo de 100 kN atravessa essa ponte de peso linear constante de 10 kN/m. Se nos apoios B e E são instaladas molas elásticas com k = 9000 kN/m, calcule a máxima contração que surge nas molas, enquanto o veículo atravessa o trecho central CD da ponte.

Observações:
• o veículo é um objeto pontual;
• desconsidere eventuais forças horizontais que surjam na ponte; e
• considere que as deformações das molas sejam muito menores do que o comprimento da ponte.

Questão 67308

(IME - 2021/2022 2º Fase) 

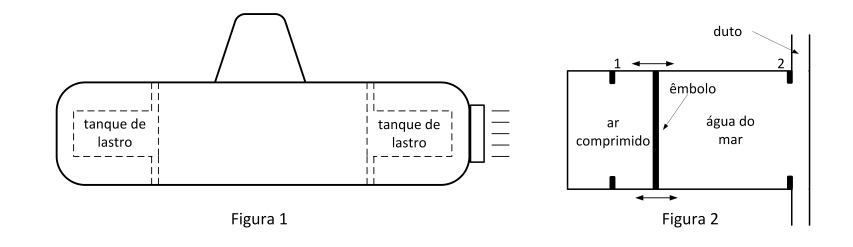
O submarino, mostrado na Figura 1, está com os tanques de lastro vazios de água e, nestas condições, possui massa específica µs = 0,92 g/cm³, quando está sem tripulação e suprimentos. Na Figura 2, ilustra-se um dos dois tanques cilíndricos de lastro idênticos, que podem ser preenchidos com água do mar. Os êmbolos são acionados por motores elétricos, sendo movimentados entre os batentes, de modo a regular o volume de água do mar nesses tanques. Considere que o tanque de lastro esteja sem água com o êmbolo na posição 2 e com 59,5 m³ de água do mar com o êmbolo na posição 1, quando estiver cheio.

Dados:

• massa específica da água do mar: µ_a = 1,03 g/cm³;

• volume do submarino: Vs = 840 m³; e

• aceleração da gravidade: g = 10 m/s².

Observação:

• os fluxos de água nos dutos dos tanques de lastro não interferem no movimento do submarino. Admitindo que, em determinada missao, embarcaram tripulantes e suprimentos, perfazendo uma massa de 5880 kg, determine:

a) a porcentagem do volume do submarino que ficará submersa após o embarque, supondo os  tanques de lastro com os êmbolos na posição 2; 

b) a massa total de água do mar, em kg, que deverá ser introduzida nos tanques de lastro para que ocorra a completa submersão do submarino; 

c) os maximos módulos das acelerações verticais, em m/s² , para emergir e para submergir o submarino, desconsiderando a forc¸a de resistência da água do mar e estando o submarino estabilizado em determinada profundidade.

Questão 67309

(IME - 2021/2022 - 2ª fase)

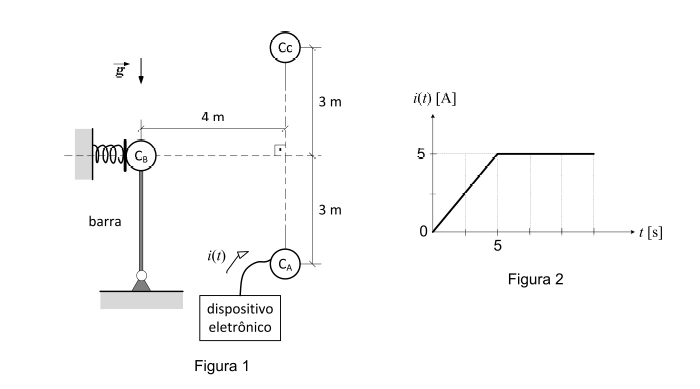
Considere um meio hipotetico onde os corpos , e todos de massa , estao fixados no espaço conforme mostra a Figura 1 e, inicialmente, carregados eletricamente com cargas ; ; e , respectivamente. O corpo esta na extremidade de uma barra feita com material isolante. Um dispositivo eletrônico controla a quantidade de cargas elétricas positivas em , por meio de injeção de corrente no corpo.

Dados:

• aceleração da gravidade: ; e
• massa dos corpos: .

Considerações:

• o fluxo positivo de corrente do grafico da Figura 2 indica que cargas positivas são injetadas em ; e
• a mola tem por objetivo manter a barra sempre na posição vertical.

Diante do exposto, determine:

a) a constante eletrostática do meio, sabendo que nas condições iniciais, a força de compressão na barra é 4 N.

Considere agora que o dispositivo eletrônico comece a operar, injetando corrente no corpo (conforme grafico da Figura 2) até que a tração na barra seja 0 (zero). Para as novas condições de funcionamento, determine:

b) o novo valor da carga ; e

c) o tempo necessário para o sistema chegar a este novo ponto de operação.

Questão 67310

(IME - 2021/2022 - 2ª fase) 

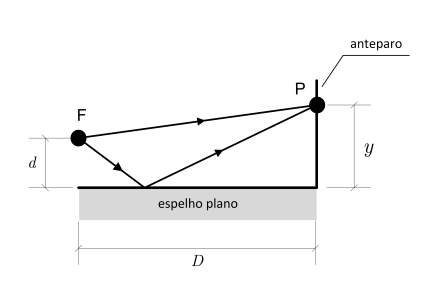
No espelho de Lloyd, observa-se em um anteparo a interferência entre a luz que vai da fonte puntiforme F a um ponto P do anteparo e a luz que vai de F a P, após ser refletida num espelho plano. A distância de F ao espelho é d e de F ao anteparo é D.

Dados:

• comprimento de onda da luz: λ; e

• D ≫ d.

Consideração:

• , se  |u| ≪ 1 (se necessário)

Diante do exposto, determine o menor valor de y, indicado na figura, para que no ponto P haja um máximo de interferência construtiva.

Questão 67347

(IME - 2021/2022 - 2ª fase)

Sob determinadas condições, a água pode ser super-resfriada, ou seja, permanecer no estado líquido em temperaturas inferiores ao se ponto de congelamento, em uma situação termodinamicamente instável. Considere um processo em que 5,0 mol de água super-resfriada a -10°C e 1,0 atm sejam convertidos em gelo à mesma temperatura. Determine a variação de entropia:

a) do sistema;

b) na vizinhança. e

c) do universo 

Dados: