ITA 2023
Questão 76058
ITA
(ITA - 2023 - 1ª FASE)
Em uma determinada temperatura, uma mistura gasosa contendo as substâncias X, Y2 e XY é adicionada a um recipiente de 1 L, nas concentrações, em mol L–1, de 0,4, 0,4 e 0,8, respectivamente. A equação química que representa a reação, cuja constante de equilíbrio é igual a 16, é dada por
Assinale a opção que contém a concentração aproximada, em mol L–1, do produto XY, após a reação atingir o equilíbrio.
Ver questãoQuestão 76059
ITA
(ITA - 2023 - 1ª FASE)
Considere que valores maiores de energia de hidratação são observados para íons com menor tamanho e maior carga. Com base nessa informação, são feitas as seguintes comparações entre a energia de hidratação dos pares de íons abaixo.
I. Li+ > K+.
II. B3+ > Al3+.
III. Sr2+ < Ca2+.
IV. Ga3+ > Ca2+.
V. S2- > Se2-.
Das comparações I a V, acima destacadas, são CORRETAS
Ver questãoQuestão 76060
ITA
(ITA - 2023 - 1ª FASE)
Considere as seguintes afirmações sobre características de óleos e gorduras.
I. Em temperatura ambiente, óleos são líquidos e gorduras são sólidas.
II. Óleos são ricos em ésteres de ácidos graxos insaturados, ao passo que gorduras possuem predominância de ésteres de ácidos graxos saturados.
III. A reação entre óleos ou gorduras com hidróxido de sódio (NaOH) ou hidróxido de potássio (KOH) produz sabão.
IV. Quanto maior é o índice de saponificação, maior a massa molar média do triglicerídeo do óleo ou da gordura. Por índice de saponificação, entenda-se a massa de KOH, em mg, necessária para saponificar 1 g de óleo ou de gordura.
Das afirmações I a IV, acima destacadas, são CORRETAS
Ver questãoQuestão 76061
ITA
(ITA - 2023 - 1ª FASE)
Considere as seguintes afirmações relativas a ácidos.
I. O ácido fosfórico possui hidrogênios que podem ser substituídos por grupos orgânicos para a formação de ésteres.
II. O ácido fosfórico pode produzir três cátions do tipo hidroxônio em água.
III. A ionização do ácido clorídrico aumenta a condutividade elétrica de soluções aquosas.
IV. O grau de ionização de ácidos é a relação entre o número de moléculas dissolvidas e o número total de moléculas.
Das afirmações I a IV, acima destacadas, são CORRETAS
Ver questãoQuestão 76062
ITA
(ITA - 2023 - 1ª FASE)
Os seguintes diagramas representam diferentes estados de equilíbrio de uma reação exotérmica do tipo

Assinale a opção que contém a afirmação CORRETA.
Ver questãoQuestão 76400
ITA
(ITA - 2023 - 2ª FASE)
Um bloco cúbico de aresta l = 4,5 cm desliza, sob o efeito da gravidade, sobre um plano inclinado de ângulo relativamente à horizontal. O deslizamento acontece com as normais de duas de suas faces sempre paralelas à direção do movimento. Para estudar o movimento, um observador usa uma máquina fotográfica que captura em uma mesma imagem a posição do bloco em instantes diferentes. Para isso, a câmera é programada para abrir e fechar o diafragma periodicamente, a cada intervalo de tempo
. O tempo de exposição
, isto é, o tempo em que o diafragma permanece aberto, é tal que
. O disparo da câmera é sincronizado com o movimento, de modo que a primeira exposição acontece no instante em que o bloco é solto. A foto registra quatro pontos, que correspondem à posição do objeto em diferentes instantes. O experimentador extrai da foto a distância entre pontos adjacentes,
, com n = 1, 2 e 3.
Considere que a foto capta o perfil lateral do plano inclinado sem distorrções ópticas ou efeitos de paralaxe. Em seguida, faça o que se pede:
a) se , determine os valores de
,
e o deslocamento total do bloco;
b) estime o valor do coeficiente de atrito cinético entre a superfície do bloco e do plano inclinado;
c) considere agora que ainda é pequeno, mas seu efeito já não é mais desprezível. Determine o valor de
para que, na quarta captura, a imagem seja um retângulo de dimensões l por 2l.
Questão 76401
ITA
(ITA - 2023 - 2ª FASE)
Considere uma partícula , de massa
, inicialmente em repouso. Em seguida, essa partícula é acelerada por uma força constante
, durante um intervalo de tempo
. Após este intervalo de tempo,
move-se livremente sem atrito por um plano, até colidir com uma partícula
, de massa
. Após a colisão,
sai em uma trajetória que faz um ângulo de
com relação à trajetória inicial (pré-colisão) de
. Após um breve deslocamento, uma força constante
, com direção contrária à da velocidade da partícula
, atua durante um intervalo de tempo
atéa parada total de
.
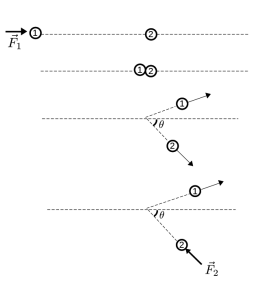
Sabendo que a colisão entre e
é inelástica e resulta em uma perda de 25% da energia mecânica do sistema, determine a magnitude da força
em termos da magnitude de
.
Questão 76402
ITA
(ITA - 2023 - 2ª FASE)
Considere um recipiente que contém uma coluna de água de altura H. Um pequeno furo é feito na parede a uma altura h, de tal forma que um filete de água é expelido horizontalmente, como na figura. Considere a água um fluido incompressível e de viscosidade desprezível. A aceleração local da gravidade vale g.
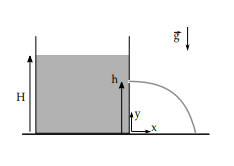
Determine:
a) a trajetória y(x) do filete de água descrito;
b) o lugar geométrico dos pontos P(x, y) que podem ser atingidos por um filete de água, considerando que a altura h possa ser escolhida entre 0 e H.
Ver questãoQuestão 76403
ITA
(ITA - 2023 - 2ª FASE)
Considere uma nave espacial esférica, de raio , com paredes de espessura
. No espaço profundo, existe uma radiação cósmica de fundo de temperatura
(aproximadamente 2,7 K). Seja a temperatura da parede interna da nave
, e a temperatura da parede externa
, com
. A condutividade térmica do material que compõe a parede da nave é
; o seu calor específico é
e sua densidade de massa é
. A emissividade da nave é unitária e a constante de Stefan-Boltzmann é dada por
. Quando ocorrem pequenas variações de temperatura na parede interna da nave, a condição de fluxo estacionário de calor é perturbada e o sistema tende a uma nova situação de fluxo estacionário de energia. A constante de tempo característica
desse processo pode ser estimada apenas em termos das características do material que compõem o revestimento da nave –
,
e
– bem como sua espessura
.
Faça o que se pede:
a) obtenha a equação polinomial cuja raiz forneça com os coeficientes em termos de
, considerando a condição de fluxo de calor estacionário;
b) estime, por análise dimensional, uma expressão para .
Questão 76404
ITA
(ITA - 2023 - 2ª FASE)
Um emissor de onda sonora esférica de frequência executa um movimento circular uniforme com velocidade angular
e raio
em torno da origem
do plano
, de acordo com a figura. Ao mesmo tempo, um receptor sonoro executa um movimento no eixo y de forma que sua posição sempre coincida com a coordenada y do emissor. A velocidade do som é designada como
. Sabe-se que o gráfico da frequência da onda sonora detectada no receptor, f
, em função da coordenada x do emissor, aproxima-se de uma cônica para o caso em que
.
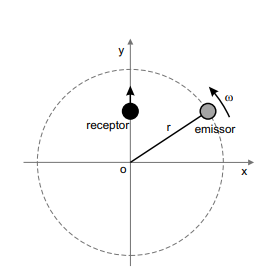
Determine:
a) a velocidade máxima alcançada pelo receptor;
b) a cônica e sua equação.
Ver questão